题目内容
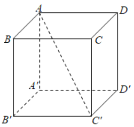
【题目】已知四边形ABCD为矩形,AB=2AD=4,M为AB的中点,将△ADM沿DM折起,得到四棱锥A1﹣DMBC,设A1C的中点为N,在翻折过程中,得到如下有三个命题:①BN∥平面A1DM;②三棱锥N﹣DMC的最大体积为![]() ;③在翻折过程中,存在某个位置,使得DM⊥A1C.其中正确命题的序号为_____.
;③在翻折过程中,存在某个位置,使得DM⊥A1C.其中正确命题的序号为_____.
【答案】①②
【解析】
分别延长DM,CB交于H,连接A1H,可证B为CH的中点,因此有BN∥A1H,可得①为正确;要使三棱锥N﹣DMC的体积最大,只需N到平面DMBC的距离最大,当平面A1DM⊥平面DMBC时满足,可求得此时体积为![]() ,②正确;DM=CM=2,CD=4,
,②正确;DM=CM=2,CD=4,
可得DM⊥MC,若DM⊥A1C,可证DM⊥A1M,与已知DM为斜边矛盾,③错误.
对于①,分别延长DM,CB交于H,连接A1H,如图所示;
由已知得![]() ,可得B为CH的中点,
,可得B为CH的中点,
可得BN为△A1CH的中位线,可得BN∥A1H,
BN平面A1DM,A1H平面A1DM,
可得BN∥平面A1DM∴①正确;
对于②,当平面A1DM⊥平面DMBC时,
A1到平面DMBC的距离最大,且为![]() ,
,
此时N到平面DMBC的距离最大,且为![]() ,
,
△DMC的面积为![]() 2×4=4,
2×4=4,
可得三棱锥N﹣DMC的最大体积为![]() 4
4![]() ,
,
∴②正确;
对于③,若DM⊥A1C,又DM=CM=2,CD=4,
可得DM⊥MC,则DM⊥平面A1CM,即有DM⊥A1M,
这与DM为斜边矛盾,∴③错误;
综上,以上正确命题的序号为①②.
故答案为:①②.


练习册系列答案
相关题目