题目内容
已知函数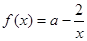 。
。
(1)讨论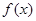 的奇偶性;
的奇偶性;
(2)判断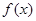 在
在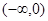 上的单调性并用定义证明。
上的单调性并用定义证明。
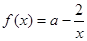 。
。(1)讨论
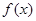 的奇偶性;
的奇偶性;(2)判断
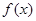 在
在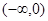 上的单调性并用定义证明。
上的单调性并用定义证明。(1) 不具备奇偶性
不具备奇偶性
(2) 在
在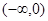 上单调递增
上单调递增
 不具备奇偶性
不具备奇偶性(2)
 在
在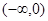 上单调递增
上单调递增试题分析:解:(1)函数
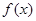 的定义域为
的定义域为 关于原点对称。 1分
关于原点对称。 1分(1)方法1:
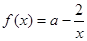 ,
,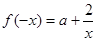 2分
2分若
 ,则
,则 ,无解,
,无解, 不是偶函数 4分
不是偶函数 4分若
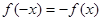 ,则
,则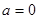 ,显然
,显然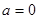 时,
时,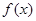 为奇函数
为奇函数综上,当
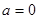 时,
时,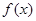 为奇函数;当
为奇函数;当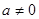 时,
时,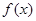 不具备奇偶性 6分
不具备奇偶性 6分方法2:函数
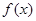 的定义域为
的定义域为 关于原点对称。 1分
关于原点对称。 1分当
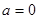 时,
时,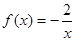 ,
, ,
,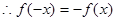 ,
, 为奇函数: 4分
为奇函数: 4分当
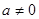 时,
时,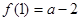 ,
,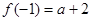 ,显然
,显然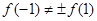
 不具备奇偶性。 6分
不具备奇偶性。 6分(2)函数
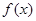 在
在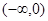 上单调递增; 7分
上单调递增; 7分证明:任取
 且
且 ,则
,则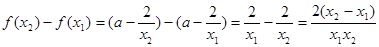 9分
9分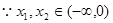 且
且 ,
, ,
,从而
 ,故
,故 , 11分
, 11分 在
在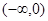 上单调递增。 12分
上单调递增。 12分点评:解决的关键是对于函数奇偶性和单调性概念的准确判定和运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
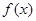 是奇函数,且当
是奇函数,且当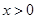 时,
时,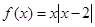 ,求
,求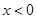 时,
时,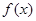 是定义在区间
是定义在区间 上的偶函数,且满足
上的偶函数,且满足
 时,
时, .求使方程
.求使方程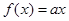 在
在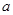 的取值集合M.
的取值集合M.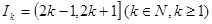 ,
, 表示使方程
表示使方程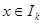 上有两个不相等实根的
上有两个不相等实根的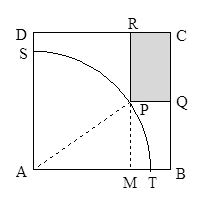
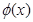 、
、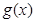 都是奇函数,
都是奇函数,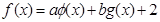 在
在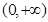 上有最大值5,则
上有最大值5,则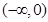 上有最小值__________。
上有最小值__________。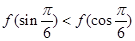
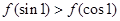

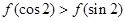
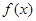 是偶函数,且当
是偶函数,且当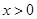 时,
时,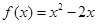 ,则当
,则当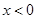 时,
时,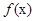 是定义在R上的以3为周期的偶函数,且
是定义在R上的以3为周期的偶函数,且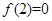 ,
,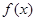 是定义在
是定义在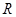 上的奇函数,给出下列命题:
上的奇函数,给出下列命题: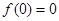 ;
;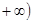 上有最小值 -1,则
上有最小值 -1,则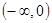 上有最大值1;
上有最大值1;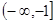 上为减函数;
上为减函数;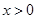 时,
时,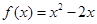 ; 则
; 则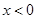 时,
时,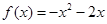 。
。