题目内容
【题目】已知函数![]() ,
, ![]() .
.
(1)若曲线![]() 的一条切线经过点
的一条切线经过点![]() ,求这条切线的方程.
,求这条切线的方程.
(2)若关于![]() 的方程
的方程![]() 有两个不相等的实数根x1,x2。
有两个不相等的实数根x1,x2。
①求实数a的取值范围;
②证明: ![]() .
.
【答案】(1)![]() 或
或![]() .(2)①
.(2)①![]() ②见解析
②见解析
【解析】试题分析:(1)先设切线点斜式方程,再与二次函数联立方程组,利用判别式为零得斜率(2)①先求函数导数,分类讨论导函数零点,单调函数至多一个零点,所以函数不单调,再依次讨论对应单调区间上有零点满足的条件②构造函数![]() ,
, ![]() ,利用导数易得函数单调递增,即得结论
,利用导数易得函数单调递增,即得结论
试题解析:解:(1)解法一 设经过点![]() 的切线与曲线
的切线与曲线![]() 相切于点
相切于点![]() ,
,
由![]() 得
得![]() ,
,
所以该切线方程为![]() ,
,
因为该切线经过![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以切线方程为![]() 或
或![]() .
.
解法二 由题意得曲线![]() 的切线的斜率一定存在,
的切线的斜率一定存在,
设所求的切线方程为![]() ,
,
由 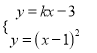 ,得
,得![]() ,
,
因为切线与抛物线相切,
所以![]() ,解得
,解得![]() ,
,
所以所求的切线方程为![]() 或
或![]() .
.
(2)①由![]() ,得
,得![]() .
.
设![]() ,
,
则![]() ,
,
由题意得函数![]() 恰好有两个零点.
恰好有两个零点.
(i)当![]() ,则
,则![]() ,
,
![]() 只有一个零点1.
只有一个零点1.
(ii)当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
即![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
而![]() ,
,
所以![]() 在
在![]() 上有唯一零点,且该零点在
上有唯一零点,且该零点在![]() 上.
上.
取![]() 且
且![]() ,
,
则![]()
所以![]() 在
在![]() 上有唯一零点,且该零点在
上有唯一零点,且该零点在![]() 上,
上,
所以![]() 恰好有两个零点.
恰好有两个零点.
(iii)当![]() 时,由
时,由![]() 得
得![]() ,
,
若![]() ,
, ![]() ,
,
所以![]() 在
在![]() 上至多有一个零点.
上至多有一个零点.
若![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,所以
,所以![]() 在
在![]() 上至多有一个零点.
上至多有一个零点.
当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上为减函数,
上为减函数,
又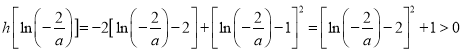 ,
,
所以h(x)在![]() 上无零点.
上无零点.
若![]() ,则
,则![]() ,
,
又当![]() 时,
时, ![]() ,
,
所以![]() 不存在零点.
不存在零点.
![]() 在
在![]() 上无零点
上无零点
故当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
因此![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
又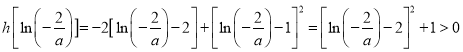 。
。
所以![]() 在
在![]() 无零点,在
无零点,在![]() 至多有一个零点.
至多有一个零点.
综上, ![]() 的取值范围为
的取值范围为![]() .
.
②不妨设![]() ,
,
由①知![]() ,
, ![]() ,且
,且![]() ,
, ![]() 在
在![]() 单调递减,
单调递减,
所以![]() 等价于
等价于![]() ,即
,即![]() .
.
由于![]() ,
,
且![]() ,
,
所以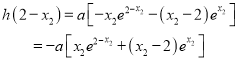 .
.
设![]() ,
,
则![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() .
.
而![]() ,故当
,故当![]() 时,
时, ![]() .
.
从而![]() ,故
,故![]() .
.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案【题目】2018年7月24日,长春长生生物科技有限责任公司先被查出狂犬病疫苗生产记录造假,因此,疫苗在上市前必须经过严格的检测,以保证疫苗使用的安全和有效.某生物制品研究所将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如表:现从所有试验小白鼠中任取一只,取到“注射疫苗”小白鼠的概率为![]() .
.
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 20 | x | A |
注射疫苗 | 30 | y | B |
总计 | 50 | 50 | 100 |
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
(1)求2×2列联表中的数据![]() 的值;
的值;
(2)能否有99.9%把握认为注射此种疫苗有效?
附:![]() ,n=a+b+c+d.
,n=a+b+c+d.
【题目】为研究某种图书每册的成本费![]() (元)与印刷数
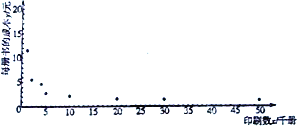
(元)与印刷数![]() (千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.
(千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
15.25 | 3.63 | 0.269 | 2085.5 |
| 0.787 | 7.049 |
表中![]() ,
, ![]() .
.
(1)根据散点图判断: ![]() 与
与![]() 哪一个更适宜作为每册成本费
哪一个更适宜作为每册成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的回归方程类型?(只要求给出判断,不必说明理由)
(千册)的回归方程类型?(只要求给出判断,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
(3)若每册书定价为10元,则至少应该印刷多少册才能使销售利润不低于78840元?(假设能够全部售出,结果精确到1)
(附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为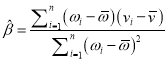 ,
, ![]() )
)