题目内容
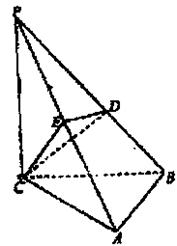
(本题满分14分)如图,三棱锥P—ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB。(1)求证:AB 平面PCB;(2)求二面角C—PA—B的大小.
平面PCB;(2)求二面角C—PA—B的大小.
 平面PCB;(2)求二面角C—PA—B的大小.
平面PCB;(2)求二面角C—PA—B的大小.(Ⅰ)略 (Ⅱ) arcsin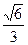
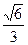
(1)∵PC 平面ABC,
平面ABC,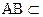 平面ABC,
平面ABC,
∴PC AB
AB
∵CD 平面PAB,
平面PAB,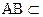 平面PAB,∴CD
平面PAB,∴CD AB又
AB又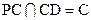 ,
,
∴AB 平面PCB.…6分
平面PCB.…6分
(2)解法一:取AP的中点E,连结CE、DE.
∵PC=AC=2,∴CE PA,CE=
PA,CE=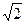 .
.
∵CD 平面PAB,
平面PAB,
由三垂线定理的逆定理,得DE PA.
PA.
∴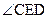 为二面角C-PA-B的平面角.
为二面角C-PA-B的平面角.
由(I) AB 平面PCB,又∵AB⊥BC,又AB=BC,AC=2,可求得BC=
平面PCB,又∵AB⊥BC,又AB=BC,AC=2,可求得BC=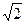 .
.
在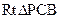 中,PB=
中,PB=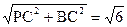 ,
,
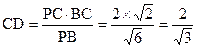 .
.
在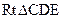 中, sin∠CED=
中, sin∠CED=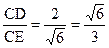 .
.
∴二面角C—PA—B的大小为arcsin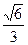 .…………14分
.…………14分
(2)解法二:
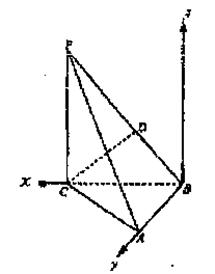
∵AB⊥BC,AB⊥平面PBC,过点B作直线l//PA,则l⊥AB,l⊥BC,以BC、BA、l所在直线为x、y、z轴建立空间直角坐标系(如图)
设平面PAB的法向量为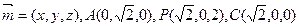
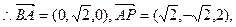
则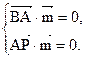 即
即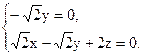

解得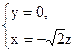
令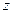 =" -1, " 得
=" -1, " 得 = (
= (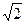 ,0,-1)
,0,-1)
设平面PAC的法向量为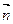 =(
=(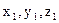 ).
).
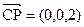 ,
,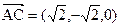 ,
,
则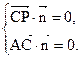 即
即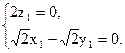
解得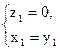 令
令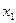 ="1, " 得
="1, " 得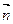 = (1,1,0).
= (1,1,0).
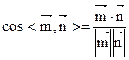 =
=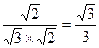
∴二面角C—PA—B的大小为arccos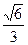
 平面ABC,
平面ABC,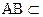 平面ABC,
平面ABC,∴PC
 AB
AB
|
 平面PAB,
平面PAB,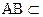 平面PAB,∴CD
平面PAB,∴CD AB又
AB又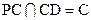 ,
,∴AB
 平面PCB.…6分
平面PCB.…6分(2)解法一:取AP的中点E,连结CE、DE.
∵PC=AC=2,∴CE
 PA,CE=
PA,CE=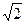 .
.∵CD
 平面PAB,
平面PAB,由三垂线定理的逆定理,得DE
 PA.
PA.∴
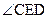 为二面角C-PA-B的平面角.
为二面角C-PA-B的平面角.由(I) AB
 平面PCB,又∵AB⊥BC,又AB=BC,AC=2,可求得BC=
平面PCB,又∵AB⊥BC,又AB=BC,AC=2,可求得BC=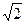 .
.在
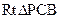 中,PB=
中,PB=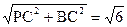 ,
,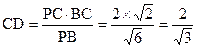 .
.在
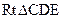 中, sin∠CED=
中, sin∠CED=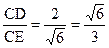 .
.∴二面角C—PA—B的大小为arcsin
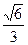 .…………14分
.…………14分(2)解法二:
∵AB⊥BC,AB⊥平面PBC,过点B作直线l//PA,则l⊥AB,l⊥BC,以BC、BA、l所在直线为x、y、z轴建立空间直角坐标系(如图)
|
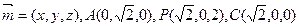
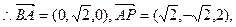
则
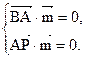 即
即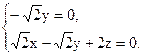

解得
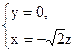
令
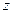 =" -1, " 得
=" -1, " 得 = (
= (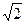 ,0,-1)
,0,-1)设平面PAC的法向量为
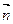 =(
=(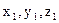 ).
).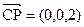 ,
,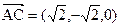 ,
,则
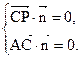 即
即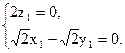
解得
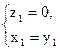 令
令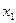 ="1, " 得
="1, " 得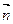 = (1,1,0).
= (1,1,0).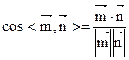 =
=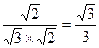
∴二面角C—PA—B的大小为arccos
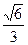

练习册系列答案
相关题目
 ,BB1=2,∠ABC=90°,E、F分为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度是________.
,BB1=2,∠ABC=90°,E、F分为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度是________. 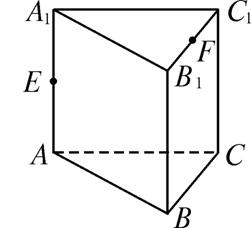
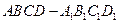 中,
中,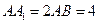 ,点
,点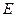 在
在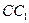 上
上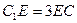 .
.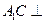 平面
平面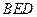 ;(2)求二面角
;(2)求二面角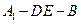 的大小.
的大小.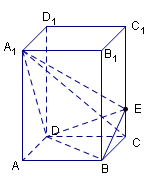
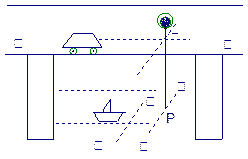
 X∥Y”为真命题的是_________(填序号)
X∥Y”为真命题的是_________(填序号)
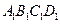 的棱长为l,点F、H分别为为
的棱长为l,点F、H分别为为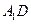 、A1C的中点.
、A1C的中点.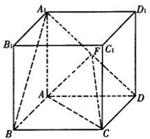
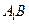 ∥平面AFC;.
∥平面AFC;. 平面AFC.
平面AFC.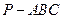 高为2,侧棱与底面所成角为
高为2,侧棱与底面所成角为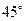 ,则点
,则点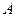 到侧面
到侧面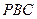 的距离是
的距离是 的平面去截球,所得的截面面积为
的平面去截球,所得的截面面积为 ,则球的体积为( )
,则球的体积为( )


