题目内容
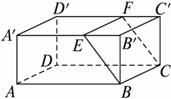
如图,正四棱柱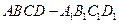 中,
中,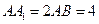 ,点
,点 在
在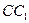 上
上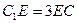 .
.
(1)证明: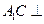 平面
平面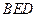 ;(2)求二面角
;(2)求二面角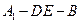 的大小.
的大小.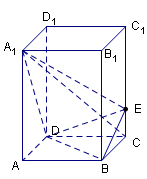
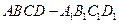 中,
中,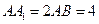 ,点
,点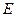 在
在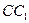 上
上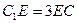 .
.(1)证明:
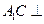 平面
平面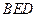 ;(2)求二面角
;(2)求二面角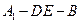 的大小.
的大小.
解法一: ,
依题设知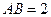 ,
,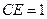 .
.
(Ⅰ)连结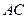 交
交 于点
于点 ,则
,则 .
.
由三垂线定理知, .······························································· 3分
.······························································· 3分
在平面 内,连结
内,连结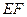 交
交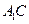 于点
于点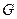 ,
,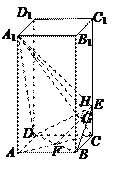
由于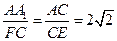 ,
,
故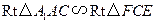 ,
,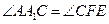 ,
,
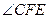 与
与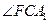 互余.
互余.
于是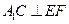 .
.
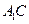 与平面
与平面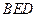 内两条相交直线
内两条相交直线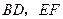 都垂直,
都垂直,
所以
 平面
平面 .········································································· 6分
.········································································· 6分
(Ⅱ)作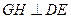 ,垂足为
,垂足为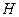 ,连结
,连结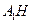 .由三垂线定理知
.由三垂线定理知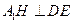 ,
,
故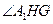 是二面角
是二面角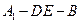 的平面角.··············································· 8分
的平面角.··············································· 8分
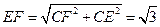 ,
,
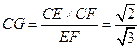 ,
,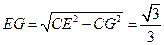 .
.
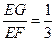 ,
,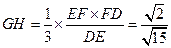 .
.
又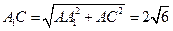 ,
,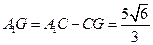 .
.
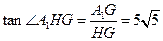 .
.
 所以二面角
所以二面角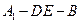 的大小为
的大小为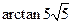 .··············· 12分
.··············· 12分
解法二:
以 为坐标原点,射线
为坐标原点,射线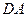 为
为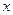 轴的正半轴,
轴的正半轴,
建立如图所示直角坐标系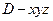 .
.
依题设,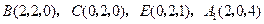 .
.
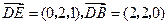 ,
,
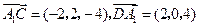 .······························································· 3分
.······························································· 3分
(Ⅰ)因为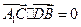 ,
,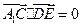 ,
,
故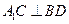 ,
, .
.
又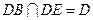 ,
,
所以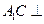 平面
平面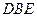 .········································································· 6分
.········································································· 6分
(Ⅱ)设向量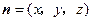 是平面
是平面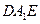 的法向量,则
的法向量,则
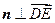 ,
,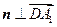 .
.
故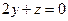 ,
,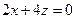 .
.
令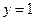 ,则
,则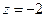 ,
,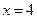 ,
,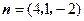 .·············································· 9分
.·············································· 9分
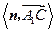 等于二面角
等于二面角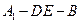 的平面角,
的平面角,
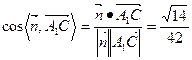 .
.
所以二面角 的大小为
的大小为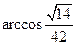 .
.
依题设知
 ,
,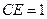 .
.(Ⅰ)连结
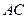 交
交 于点
于点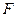 ,则
,则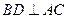 .
.由三垂线定理知,
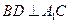 .······························································· 3分
.······························································· 3分在平面
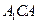 内,连结
内,连结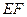 交
交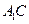 于点
于点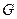 ,
,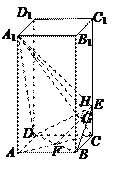
由于
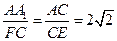 ,
,故
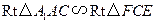 ,
,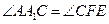 ,
,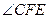 与
与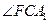 互余.
互余.于是
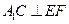 .
.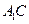 与平面
与平面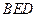 内两条相交直线
内两条相交直线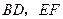 都垂直,
都垂直,所以
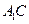
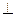 平面
平面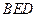 .········································································· 6分
.········································································· 6分(Ⅱ)作
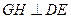 ,垂足为
,垂足为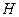 ,连结
,连结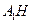 .由三垂线定理知
.由三垂线定理知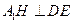 ,
,故
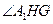 是二面角
是二面角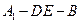 的平面角.··············································· 8分
的平面角.··············································· 8分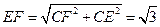 ,
,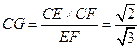 ,
,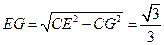 .
.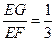 ,
,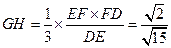 .
.又
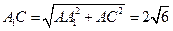 ,
,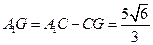 .
.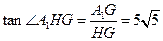 .
. 所以二面角
所以二面角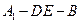 的大小为
的大小为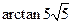 .··············· 12分
.··············· 12分解法二:
以
 为坐标原点,射线
为坐标原点,射线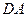 为
为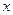 轴的正半轴,
轴的正半轴,建立如图所示直角坐标系
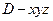 .
.依题设,
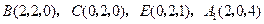 .
.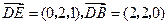 ,
,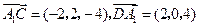 .······························································· 3分
.······························································· 3分(Ⅰ)因为
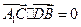 ,
,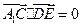 ,
,故
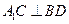 ,
, .
.又
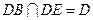 ,
,所以
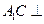 平面
平面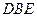 .········································································· 6分
.········································································· 6分(Ⅱ)设向量
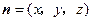 是平面
是平面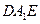 的法向量,则
的法向量,则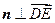 ,
,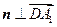 .
.故
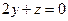 ,
,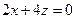 .
.令
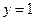 ,则
,则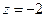 ,
,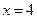 ,
,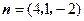 .·············································· 9分
.·············································· 9分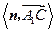 等于二面角
等于二面角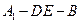 的平面角,
的平面角,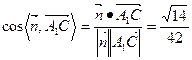 .
.所以二面角
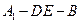 的大小为
的大小为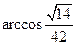 .
.同答案

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 与直线
与直线
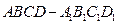 中,
中,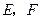 分别是
分别是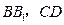 的中点.
的中点.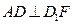 ;
;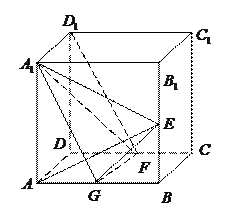 (2)求
(2)求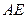 与
与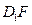 所成的角;
所成的角;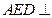 面
面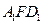 ;
;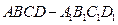 中,
中,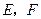 分别为
分别为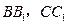 的中点.求
的中点.求 所成角的余弦值.
所成角的余弦值.
 平面PCB;(2)求二面角C—PA—B的大小.
平面PCB;(2)求二面角C—PA—B的大小. 中,
中,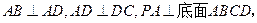
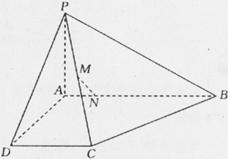
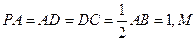 为
为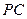 的中点,
的中点,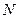 点在
点在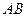 上且
上且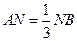
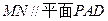 N;
N;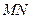 与平面
与平面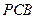 所成的角
所成的角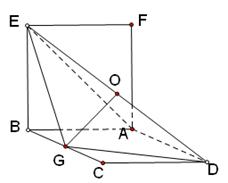 如图,正方形
如图,正方形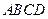 和
和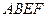 的边长均为1,且它们所在平面互相垂直,
的边长均为1,且它们所在平面互相垂直,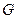 为线段
为线段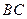 的中点,
的中点, 为线段
为线段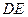 的中点。
的中点。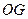 ∥面
∥面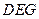 ⊥平面
⊥平面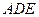 ;
;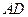 与平面
与平面