题目内容
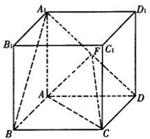
正方体.ABCD- 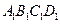 的棱长为l,点F、H分别为为
的棱长为l,点F、H分别为为 、A1C的中点.
、A1C的中点.
(1)证明: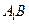 ∥平面AFC;.
∥平面AFC;.
(2)证明B1H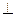 平面AFC.
平面AFC.
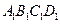 的棱长为l,点F、H分别为为
的棱长为l,点F、H分别为为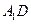 、A1C的中点.
、A1C的中点.
(1)证明:
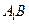 ∥平面AFC;.
∥平面AFC;.(2)证明B1H
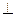 平面AFC.
平面AFC.同下
解:(1)连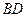 交
交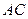 于点
于点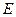 ,则
,则 的中点,所以
的中点,所以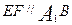 ,又因为
,又因为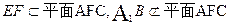 ,由下面平行的判定定理可得
,由下面平行的判定定理可得
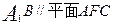
(2)连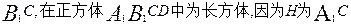 的中点,
的中点,
所以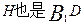 的中点,所以只要
的中点,所以只要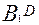 证平面
证平面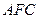 即可
即可
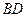 交
交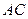 于点
于点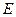 ,则
,则 的中点,所以
的中点,所以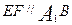 ,又因为
,又因为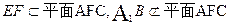 ,由下面平行的判定定理可得
,由下面平行的判定定理可得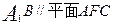
(2)连
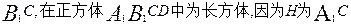 的中点,
的中点,所以
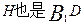 的中点,所以只要
的中点,所以只要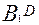 证平面
证平面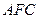 即可
即可
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
,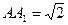 ,
, ,若
,若 为棱
为棱 中点.
中点. ∥平面
∥平面 ;
;
 与平面
与平面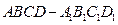 中,
中,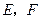 分别为
分别为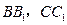 的中点.求
的中点.求 所成角的余弦值.
所成角的余弦值. 平面PCB;(2)求二面角C—PA—B的大小.
平面PCB;(2)求二面角C—PA—B的大小.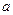 .
.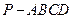 中,
中,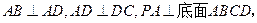
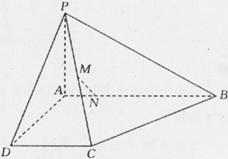
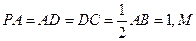 为
为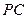 的中点,
的中点,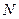 点在
点在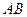 上且
上且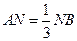
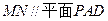 N;
N;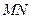 与平面
与平面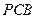 所成的角
所成的角