题目内容
【题目】某种树苗栽种时高度为A(A为常数)米，栽种n年后的高度记为f(n)．经研究发现f(n)近似地满足 f(n)＝
，其中
，a，b为常数，n∈N，f(0)＝A．已知栽种3年后该树木的高度为栽种时高度的3倍．
（1）栽种多少年后，该树木的高度是栽种时高度的8倍；
（2）该树木在栽种后哪一年的增长高度最大．
【答案】（1）栽种
年后，该树木的高度是栽种时高度的
倍；（2）第
年的增长高度最大．
【解析】
试题（1）由题中所给条件
，运用待定系数法不难求出
，进而确定出函数
，其中
．由
，运用解方程的方法即可求出
，问题得解; （2）由前面（1）中已求得
，可表示出第n年的增长高度为
，这是一个含有较多字母的式子，这也中本题的一个难点，运用代数化简和整体思想可得：
，观察此式特征能用基本不等式的方法进行求它的最值，即：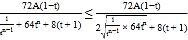
，成立的条件为 当且仅当
时取等号，即可求出
．
试题解析： （1）由题意知．
所以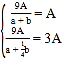
解得． 4分
所以，其中．
令，得
，解得
，
所以．
所以栽种９年后，该树木的高度是栽种时高度的8倍． 6分
（2）由（1）知．
第n年的增长高度为
． 9分
所以
12分
．
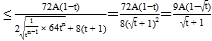当且仅当，即
时取等号，此时．
所以该树木栽种后第5年的增长高度最大． 14分
【题目】甲、乙两家外卖公司，其送餐员的日工资方案如下：甲公司的底薪70元，每单抽成4元；乙公司无底薪，40单以内（含40单）的部分每单抽成5元，超出40单的部分每单抽成7元，假设同一公司送餐员一天的送餐单数相同，现从两家公司各随机抽取一名送餐员，并分别记录其100天的送餐单数，得到如表频数表： 甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 20 | 40 | 20 | 10 | 10 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 20 | 20 | 40 | 10 |
（Ⅰ）现从甲公司记录的100天中随机抽取两天，求这两天送餐单数都大于40的概率；
（Ⅱ）若将频率视为概率，回答下列问题：
（i）记乙公司送餐员日工资为X（单位：元），求X的分布列和数学期望；
（ii）小明拟到甲、乙两家公司中的一家应聘送餐员，如果仅从日工资的角度考虑，请利用所学的统计学知识为他作出选择，并说明理由．