题目内容
【题目】已知函数y=f(x)(x∈R),对函数y=g(x)(x∈R),定义g(x)关于f(x)的“对称函数”为函数y=h(x)(x∈R),y=h(x)满足:对任意x∈R,两个点(x,h(x)),(x,g(x))关于点(x,f(x))对称.若h(x)是g(x)= ![]() 关于f(x)=3x+b的“对称函数”,且h(x)>g(x)恒成立,则实数b的取值范围是 .
关于f(x)=3x+b的“对称函数”,且h(x)>g(x)恒成立,则实数b的取值范围是 .
【答案】(2 ![]() ,+∞)
,+∞)
【解析】解:根据“对称函数”的定义可知, ![]() ,
,
即h(x)=6x+2b﹣ ![]() ,
,
若h(x)>g(x)恒成立,
则等价为6x+2b﹣ ![]() >
> ![]() ,
,
即3x+b> ![]() 恒成立,
恒成立,
设y1=3x+b,y2= ![]() ,
,
作出两个函数对应的图象如图,
当直线和上半圆相切时,圆心到直线的距离d= ![]() ,
,
即|b|=2 ![]() ,
,
∴b=2 ![]() 或﹣2
或﹣2 ![]() ,(舍去),
,(舍去),
即要使h(x)>g(x)恒成立,
则b>2 ![]() ,
,
即实数b的取值范围是(2 ![]() ,+∞),
,+∞),
所以答案是:(2 ![]() ,+∞)
,+∞)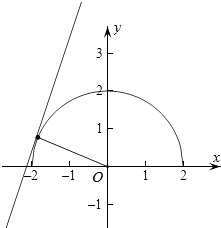

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
作物产量(kg) | 300 | 500 |
概率 | 0.5 | 0.5 |
作物市场价格(元/kg) | 6 | 10 |
概率 | 0.4 | 0.6 |
(1)设X表示在这块地上种植1季此作物的利润,求X的分布列;
(2)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2000元的概率.
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程![]()
(3)试预测加工10个零件需要多少小时?

