题目内容
正三棱锥 中,
中,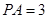 ,
, ,则
,则 与平面
与平面 所成角的余弦值为
所成角的余弦值为
 中,
中,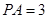 ,
, ,则
,则 与平面
与平面 所成角的余弦值为
所成角的余弦值为A.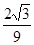 | B. | C. | D. . . |
A
设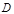 为
为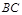 中点,显然
中点,显然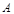 点在平面
点在平面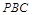 的射影
的射影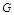 在直线
在直线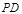 上,
上,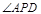 即为所求的角,在三角形
即为所求的角,在三角形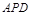 中,
中,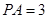 ,
,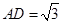 ,
,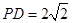 ,由余弦定理即得
,由余弦定理即得 与平面
与平面 所成角的余弦值为
所成角的余弦值为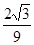 。
。
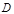 为
为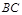 中点,显然
中点,显然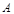 点在平面
点在平面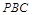 的射影
的射影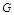 在直线
在直线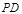 上,
上,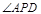 即为所求的角,在三角形
即为所求的角,在三角形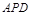 中,
中,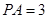 ,
,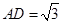 ,
,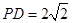 ,由余弦定理即得
,由余弦定理即得 与平面
与平面 所成角的余弦值为
所成角的余弦值为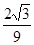 。
。
练习册系列答案
相关题目
题目内容
 中,
中,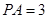 ,
, ,则
,则 与平面
与平面 所成角的余弦值为
所成角的余弦值为A.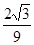 | B. | C. | D. . . |
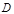 为
为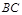 中点,显然
中点,显然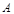 点在平面
点在平面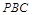 的射影
的射影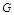 在直线
在直线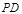 上,
上,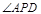 即为所求的角,在三角形
即为所求的角,在三角形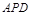 中,
中,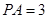 ,
,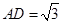 ,
,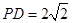 ,由余弦定理即得
,由余弦定理即得 与平面
与平面 所成角的余弦值为
所成角的余弦值为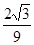 。
。