题目内容
一个赛跑机器人有如下特性:
(1)步长可以人为地设置成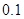 米,
米,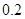 米,
米,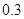 米,…,
米,…,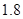 米或
米或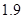 米;
米;
(2)发令后,机器人第一步立刻迈出设置的步长,且每一步的行走过程都在瞬时完成;
(3)当设置的步长为 米时,机器人每相邻两个迈步动作恰需间隔
米时,机器人每相邻两个迈步动作恰需间隔 秒.
秒.
则这个机器人跑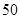 米(允许超出
米(允许超出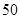 米)所需的最少时间是【 】.
米)所需的最少时间是【 】.
A.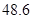 秒 秒 | B.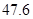 秒 秒 | C.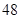 秒 秒 | D.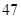 秒 秒 |
A
解析试题分析:根据题意,由于当设置的步长为 米时,机器人每相邻两个迈步动作恰需间隔
米时,机器人每相邻两个迈步动作恰需间隔 秒.这个机器人跑
秒.这个机器人跑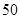 米(允许超出
米(允许超出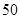 米)所需的最少时间,则说明了迈出的步长可以设置为1.9,然后借助于等差数列的通项公式可知,当50=1.9t,可知事件最小值为48.6,故选A.
米)所需的最少时间,则说明了迈出的步长可以设置为1.9,然后借助于等差数列的通项公式可知,当50=1.9t,可知事件最小值为48.6,故选A.
考点:数列的运用
点评:解决的关键是理解机器人跑n米所用的时间的最小值问题,属于基础题。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
若数列{an}的通项公式是 ,则该数列的第五项为( )
,则该数列的第五项为( )
| A.1 | B.-1 | C. | D.- |
已知等比数列 中,公比
中,公比 若
若 则
则 有( )
有( )
| A.最小值-4 | B.最大值-4 | C.最小值12 | D.最大值12 |
已知数列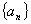 的
的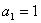 ,且
,且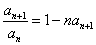 ,则此数列
,则此数列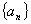 的通项公式为( )
的通项公式为( )
A.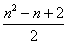 | B.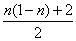 |
C.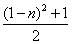 | D.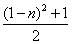 或 或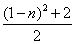 |
1202年,意大利数学家斐波那契在他的书中给出了一个关于兔子繁殖的递推关系: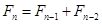 (
( ),其中
),其中 表示第
表示第 个月的兔子的总对数,
个月的兔子的总对数, ,则
,则 的值为( )
的值为( )
| A.13 | B.21 | C.34 | D.55 |
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第 行有
行有 个数且两端的数均为
个数且两端的数均为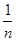
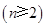 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如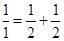 ,
,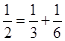 ,
,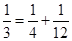 ,…,则第7行第4个数(从左往右数)为( )
,…,则第7行第4个数(从左往右数)为( )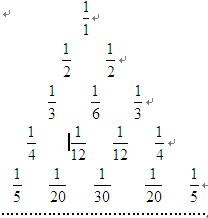
A.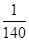 | B.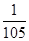 | C.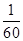 | D.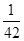 |
已知数列 ,
, ,
, ,且
,且 ,则数列的第五项为( )
,则数列的第五项为( )
A. | B. | C. | D. |
 的前
的前 项和
项和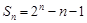
 ,则
,则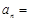 .
.