题目内容
18. 如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.
如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.(Ⅰ)求证:AB=AC;
(Ⅱ)若AB⊥AC,三棱柱的高为1,求C1点到截面A1BC的距离.
分析 (Ⅰ)取BC中点O,连OA,OA1.证明BC⊥平面A1OA,即可证明:AB=AC;
(Ⅱ)利用等体积法,即可求C1点到截面A1BC的距离.
解答 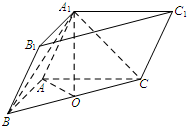 (Ⅰ)证明:取BC中点O,连OA,OA1.
(Ⅰ)证明:取BC中点O,连OA,OA1.
因为侧面BCC1B1是矩形,所以BC⊥BB1,BC⊥AA1,
因为截面A1BC是等边三角形,所以BC⊥OA1,
所以BC⊥平面A1OA,BC⊥OA,因此,AB=AC.…(5分)
(Ⅱ)解:设点A到截面A1BC的距离为d,
由VA-A1BC=VA1-ABC得S△A1BC×d=S△ABC×1,
得BC×OA1×d=BC×OA×1,得d=$\frac{OA}{OA1}$.
由AB⊥AC,AB=AC得OA=$\frac{1}{2}$BC,
又OA1=$\frac{\sqrt{3}}{2}$BC,故d=$\frac{\sqrt{3}}{3}$.
因为点A与点C1到截面A1BC的距离相等,
所以点C1到截面A1BC的距离为$\frac{\sqrt{3}}{3}$.…(12分)
点评 本题考查线面垂直的判定与性质,考查等体积法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.已知双曲线C1:$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1({a>0,b>0})$的离心率为2,若抛物线C2:y2=2px(p>0)的焦点到双曲线C1的渐近线的距离是2,则抛物线C2的方程是( )
| A. | y2=8x | B. | y2=$\frac{{16\sqrt{3}}}{3}$x | C. | y2=$\frac{{8\sqrt{3}}}{3}$x | D. | y2=16x |
10.已知在△ABC中,a,b,c分别为角A,B,C所对的边,且cosC=$\frac{2}{3}$,$\overrightarrow{AC}$•$\overrightarrow{CB}$=-2,且a+b=$\sqrt{26}$,则c边长为( )
| A. | $\sqrt{5}$ | B. | 4 | C. | $\sqrt{13}$ | D. | $\sqrt{17}$ |
8.若以直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,已知直线l参数方程为$\left\{\begin{array}{l}{x=2+t}\\{y=1-t}\end{array}\right.$(t为参数),曲线C的极坐标方程为ρ=4sinθ,则直线l被曲线C截得的弦长为( )
| A. | $\frac{\sqrt{14}}{2}$ | B. | $\sqrt{14}$ | C. | $\frac{\sqrt{7}}{2}$ | D. | $\sqrt{7}$ |
 如图,半圆的直径AB=2,D是半圆弧上一点,DC与半圆相切,且DC=2,设∠BAD=α.
如图,半圆的直径AB=2,D是半圆弧上一点,DC与半圆相切,且DC=2,设∠BAD=α. 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2.
如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2.