题目内容
9.在等比数列{an}中,a1=2,a4=16.(1)求数列{an}的通项公式和前n项和Sn;
(2)令bn=log2an2,求数列{bn}的前n项和Tn.
分析 (1)设等比数列{an}的公比为q,运用等比数列的通项公式求得q=2,再由等比数列的通项公式和求和公式计算即可得到所求;
(2)运用对数的性质,可得bn=2n,再由等差数列的求和公式,计算即可得到.
解答 解:(1)设等比数列{an}的公比为q,
由a1=2,a4=16,可得a4=a1q3,
即为2q3=16,解得q=2,
an=a1qn-1=2•2n-1=2n,
Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$=$\frac{2(1-{2}^{n})}{1-2}$=2n+1-2;
(2)bn=log2an2,=log222n=2n,
则数列{bn}的前n项和Tn=$\frac{1}{2}$(2+2n)n=n2+n.
点评 本题考查等比数列的通项公式和求和公式的运用,同时考查对数的运算性质,以及等差数列的求和公式的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
19.已知{an}是公比q>0的等比数列,a1+a2+a3=26,a5+a6+a7=2106,则首项a1=( )
| A. | 1 | B. | 2 | C. | $\frac{2}{7}$ | D. | $\frac{2}{3}$ |
20.执行如图所示的程序框图,若输入x=2,则输出y的值为( )


| A. | 23 | B. | 11 | C. | 5 | D. | 2 |
17.根据如下样本数据
得到的回归方程为$\stackrel{∧}{y}$=bx+a.若a=7.9,则b的值为-1.4.
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4.0 | 2.5 | -0.5 | 0.5 | -2.0 |
14.将6名留学归国人员分配到济南、青岛两地工作.若济南至少安排2 人,青岛至少安排3人,则不同的安排方法数为( )
| A. | 120 | B. | 150 | C. | 35 | D. | 55 |
19.已知集合A={x|-1<x<1},B={x|x2-3x≤0},则A∩B等于( )
| A. | [-1,0] | B. | (-1,3] | C. | [0,1) | D. | {-1,3} |
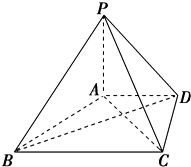 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=$\sqrt{10}$,∠DBC=45°
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=$\sqrt{10}$,∠DBC=45°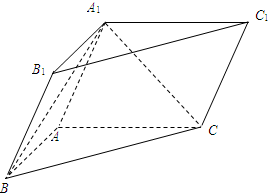 如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.
如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.