题目内容
已知不等式组 表示的平面区域为M,若直线y=kx-3k与平面区域M有公共点,则k的取值范围是( )
表示的平面区域为M,若直线y=kx-3k与平面区域M有公共点,则k的取值范围是( )
A. | B. | C. | D. |
C
解析试题分析:解:满足约束条件 的平面区域如图示:
的平面区域如图示: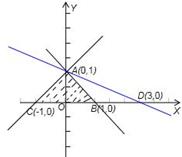
因为y=kx-3k过定点D(3,0).所以当y=kx-3k过点A(0,1)时,找到k=-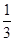 ,当y=kx-3k过点B(1,0)时,对应k=0.又因为直线y=kx-3k与平面区域M有公共点.所以-
,当y=kx-3k过点B(1,0)时,对应k=0.又因为直线y=kx-3k与平面区域M有公共点.所以-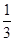 ≤k≤0.故选C.
≤k≤0.故选C.
考点:线性规划
点评:在解决线性规划的小题时,我们常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解

练习册系列答案
相关题目
设x,y满足约束条件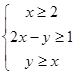 ,若目标函数
,若目标函数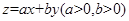 的最小值为2,则ab的最大值( )
的最小值为2,则ab的最大值( )
| A.1 | B.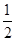 | C.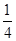 | D.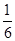 |
已知点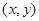 满足
满足 ,目标函数
,目标函数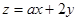 仅在点(1,0)处取得最小值,则
仅在点(1,0)处取得最小值,则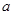 的范围为( )
的范围为( )
A.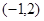 | B.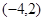 | C.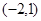 | D.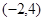 |
实数 ,
,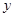 满足不等式组
满足不等式组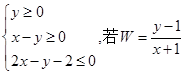 ,则有( ).
,则有( ).
A.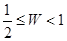 | B.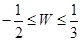 | C.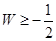 | D.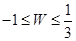 |
已知变量x、y满足的约束条件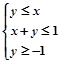 ,则
,则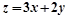 的最大值为( )
的最大值为( )
| A.-3 | B.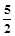 | C.-5 | D.4 |
把一根长度为7的铁丝截成任意长的3段,则能构成三角形的概率为
A. | B. | C. | D. |
设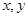 满足约束条件
满足约束条件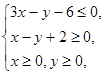 若目标函数
若目标函数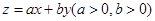 的值是最大值为12,则
的值是最大值为12,则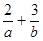 的最小值为( ).
的最小值为( ).
A.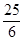 | B.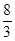 | C.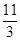 | D.4 |
点 和点
和点 在直线
在直线 的两侧,则
的两侧,则 的取值范围是( )
的取值范围是( )
A. 或 或 | B. | C. 或 或 | D. |
某所学校计划招聘男教师x名,女教师y名,x和y须满足约束条件 则该校招聘的教师人数最多是( )
则该校招聘的教师人数最多是( )
| A.10 | B.8 | C.6 | D.12 |