题目内容
某所学校计划招聘男教师x名，女教师y名，x和y须满足约束条件
则该校招聘的教师人数最多是（ ）
| A．10 | B．8 | C．6 | D．12 |
A
解析试题分析：画出线性约束条件的可行域，设该校招聘的教师人数为Z，则Z=x+y,由可行域即可求出目标函数Z=x+y的最大值为10.
考点：线性规划的简单问题。
点评：此题为易错题，主要原因是忽略了题中的隐含条件。题中的隐含条件：
.
练习册系列答案
阅读快车系列答案
相关题目
表示的平面区域为M，若直线y＝kx－3k与平面区域M有公共点，则k的取值范围是( )
变量x，y，满足约束条件
，则目标函数z=3｜x｜＋｜y－3｜的取值范围是
A．［ ，9］ | B．［－，6］ |
| C．［－2，3］ | D．［1，6］ |
已知点
在圆
上运动，则
的最大值与最小值为（ ）
A． ， | B． | C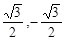． | D． |
设变量x，y满足约束条件
，则目标函数
的最大值为（ ）
| A．11 | B．10 | C．9 | D．8.5 |
设变量
满足约束条件
则目标函数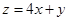
的最大值为（ ）
| A．4 | B．11 | C．12 | D．14 |
若实数
满足
，则
的最大值是（ ）
A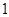． | B． | C． | D． |
设函数
，则满足
的x的取值范围是
A． ，2] | B．[0，2] | C．[1，+ ） | D．[0，+） |
设m>1，在约束条件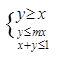
下，目标函数z＝x＋my的最大值小于2，则m的取值范围为 ( )
A．(1,1＋ ) | B．(1＋，＋∞) |
| C．(1,3) | D．(3，＋∞) |