题目内容
把一根长度为7的铁丝截成任意长的3段,则能构成三角形的概率为
A. | B. | C. | D. |
D
解析试题分析:设其中一段为 ,第二段为
,第二段为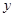 ,则第三段为
,则第三段为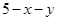 ,则利用两边之和大于第三边可以解得
,则利用两边之和大于第三边可以解得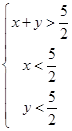 ,还有
,还有 ,画出图象,从图象上可以看出,满足不等式的三角形区域占正方形去区域的
,画出图象,从图象上可以看出,满足不等式的三角形区域占正方形去区域的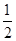 .
.
考点:本小题主要考查与面积有关的几何概型.
点评:几何概型分为与长度、角度、面积、体积等有关的几何概型,搞清楚属于那种类型,利用概率公式求解即可.

练习册系列答案
相关题目
若变量 满足约束条件
满足约束条件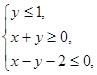 则
则 的最大值为
的最大值为
| A.4 | B.3 | C.2 | D.1 |
实数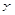 ,
,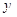 满足条件
满足条件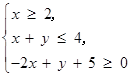 ,则目标函数
,则目标函数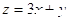 的最大值为
的最大值为
| A.7 | B.8 | C.10 | D.11 |
若变量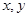 满足约束条件
满足约束条件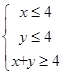 ,则目标函数
,则目标函数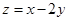 的最大值是( )
的最大值是( )
| A.2 | B.4 | C.5 | D.6 |
设 满足
满足 则
则 ( )
( )
| A.有最小值2,最大值3 | B.有最小值2,无最大值 |
| C.有最大值3,无最小值 | D.既无最小值,也无最大值 |
若实数 满足
满足 则
则 的最小值是( )
的最小值是( )
| A.-1 | B.0 | C. | D.2 |
设变量 满足约束条件
满足约束条件 则目标函数
则目标函数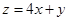 的最大值为( )
的最大值为( )
| A.4 | B.11 | C.12 | D.14 |
 表示的平面区域为M,若直线y=kx-3k与平面区域M有公共点,则k的取值范围是( )
表示的平面区域为M,若直线y=kx-3k与平面区域M有公共点,则k的取值范围是( )



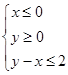 所示的平面区域,则当a从-2连续变化到1时,动直线x+ y =a扫过A中的那部分区域面积为( )
所示的平面区域,则当a从-2连续变化到1时,动直线x+ y =a扫过A中的那部分区域面积为( )
