Question

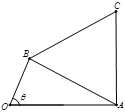
【题目】已知函数 在区间上单调递增,在区间上单调递减;如图,四边形中,,,为的内角的对边，

且满足.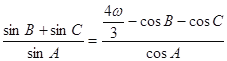

（Ⅰ）证明：；

（Ⅱ）若，设，,

，求四边形面积的最大值.

Answer 1

【答案】(1)正弦定理的运用根据边角的转换来得到证明。

(2)时取最大值,的最大值为

【解析】

试题分析：（1）利用两角和正弦公式和降幂公式化简，要熟练掌握公式，不要把符号搞错，很多同学化简不正确，求解较复杂三角函数的最值时，首先化成形式，在求最大值或最小值,寻求角与角之间的关系，化非特殊角为特殊角，灵活的掌握两角和的正弦公式进行化简；（2）在三角形中，处理三角形的边角关系时，一般全部化成角的关系，或全部化成边的关系，解决三角形问题时，注意角的范围；（3）把形如化为，可进一步研究函数的周期、单调性、最值和对称性.

试题解析：解:（1）由题意知:,解得:,

（2）因为,所以,所以为等边三角形

,

,,

当且仅当即时取最大值,的最大值为.