题目内容
【题目】设f（x）=|x﹣1|+|x+1|，（x∈R）
（1）求证：f（x）≥2；
（2）若不等式f（x）≥ 
对任意非零实数b恒成立，求x的取值范围．
【答案】
（1）证明：f（x）=|x﹣1|+|x+1|=|1﹣x|+|x+1|≥|1﹣x+x+1|=2；
（2）解：g（b）=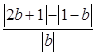 
≤ 
=3，
∴f（x）≥3，即|x﹣1|+|x+1|≥3，
x≤﹣1时，﹣2x≥3，∴x≤﹣1.5，∴x≤﹣1.5；
﹣1＜x≤1时，2≥3不成立；
x＞1时，2x≥3，∴x≥1.5，∴x≥1.5．
综上所述x≤﹣1.5或x≥1.5．
【解析】（1）利用三角不等式证明：f（x）≥2；（2）g（b）= 
≤ 
=3，可得f（x）≥3，即|x﹣1|+|x+1|≥3，分类讨论，求x的取值范围．
练习册系列答案
相关题目
【题目】2017年，嘉积中学即将迎来100周年校庆．为了了解在校同学们对嘉积中学的看法，学校进行了调查，从三个年级任选三个班，同学们对嘉积中学的看法情况如下：
对嘉积中学的看法 | 非常好，嘉积中学奠定了 | 很好，我的中学很快乐很充实 |
A班人数比例 | | |
B班人数比例 | | |
C班人数比例 | | |
（Ⅰ）从这三个班中各选一个同学，求恰好有2人认为嘉积中学“非常好”的概率（用比例作为相应概率）；
（Ⅱ）若在B班按所持态度分层抽样，抽取9人，在这9人中任意选取3人，认为嘉积中学“非常好”的人数记为ξ，求ξ的分布列和数学期望．
