Question

【题目】已知函数f（x）=ex﹣ax有极值1，这里e是自然对数的底数．
（1）求实数a的值，并确定1是极大值还是极小值；
（2）若当x∈[0，+∞）时，f（x）≥mxln（x+1）+1恒成立，求实数m的取值范围．

Answer 1

【答案】
（1）解：f′（x）=ex﹣a，∵函数f（x）=ex﹣ax有极值1，

∴存在x0，使得f′（x0）= ﹣a=0，f（x0）= ﹣ax0=1，

解得x0=0，a=1．

∴f′（x）=ex﹣1，可知：0是极小值点，因此1是极小值．

（2）解：当x∈[0，+∞）时，f（x）≥mxln（x+1）+1恒成立ex﹣x﹣1﹣mxln（x+1）≥0恒成立．

令g（x）=ex﹣（x+1），x≥0．g（0）=0．

则g′（x）=ex﹣1≥0，

∴x≥0时，函数g（x）单调递增，因此g（x）≥g（0）=0，因此ex≥x+1．

①若mxln（x+1）+x+1≤x+1，则ex﹣x﹣1﹣mxln（x+1）≥0恒成立．

则mxln（x+1）≤0，可得：m≤0．

∴m≤0时，x≥0时，f（x）≥mxln（x+1）+1恒成立．

②m＞0时，x≥0时，mxln（x+1）+x+1≤ex．

令F（x）=mxln（x+1）+x+1﹣ex，（x≥0），F（0）=0．

由F（x）≤0，可得mxln（x+1）≤ex﹣x﹣1，

x=0时，化为0≤0，恒成立，m∈R．

x＞0时，化为：m≤ ．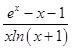

下面证明： ≤ ．

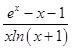令h（x）=2ex﹣2x﹣2﹣xln（x+1），h（0）=0．

h′（x）=2ex﹣2﹣ln（x+1）﹣ ．h′（0）=0．

h″（x）=2ex﹣ ﹣ ≥h″（0）=0，

∴h′（x）≥0．

∴函数h（x）在[0，+∞）上单调递增，∴h（x）≥h（0）=0．

因此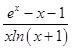： ≤ 成立，并且 是其最小值．

∴m≤ ．

综上可得：实数m的取值范围是 ．

【解析】（1）f′（x）=ex﹣a，根据函数f（x）=ex﹣ax有极值1，可得存在x0，使得f′（x0）= ﹣a=0，f（x0）= ﹣ax0=1，解得x0，a．即可判断出结论．（2）当x∈[0，+∞）时，f（x）≥mxln（x+1）+1恒成立ex﹣x﹣1﹣mxln（x+1）≥0恒成立．令g（x）=ex﹣（x+1），x≥0．g（0）=0．利用导数研究其单调性可得：ex≥x+1．①若mxln（x+1）+x+1≤x+1，则ex﹣x﹣1﹣mxln（x+1）≥0恒成立．可得：m≤0．②m＞0时，x≥0时，mxln（x+1）+x+1≤ex．令F（x）=mxln（x+1）+x+1﹣ex，（x≥0），F（0）=0．

由F（x）≤0，可得mxln（x+1）≤ex﹣x﹣1，x＞0时，化为：m≤ ．下面证明： ≤ ．利用导数研究其单调性即可得出．

【考点精析】关于本题考查的函数的极值与导数和函数的最大(小)值与导数，需要了解求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值；求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值才能得出正确答案．