题目内容
【题目】已知min{{a,b}= ![]() f(x)=min{|x|,|x+t|},函数f(x)的图象关于直线x=﹣
f(x)=min{|x|,|x+t|},函数f(x)的图象关于直线x=﹣ ![]() 对称;若“x∈[1,+∞),ex>2mex”是真命题(这里e是自然对数的底数),则当实数m>0时,函数g(x)=f(x)﹣m零点的个数为 .
对称;若“x∈[1,+∞),ex>2mex”是真命题(这里e是自然对数的底数),则当实数m>0时,函数g(x)=f(x)﹣m零点的个数为 .
【答案】4
【解析】解:∵f(x)的图象关于x=﹣ ![]() 对称,且f(0)=0,
对称,且f(0)=0,
∴f(﹣1)=0,即|﹣1+t|=0,解得t=1.
∴f(x)= 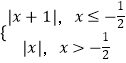 ,
,
∵对x∈[1,+∞),ex>2mex是真命题,∴m< ![]() 恒成立,x∈[1,+∞).
恒成立,x∈[1,+∞).
令h(x)= ![]() ,则h′(x)=
,则h′(x)= ![]() =
= ![]() ≥0,
≥0,
∴h(x)在[1,+∞)上单调递增,
∴hmin(x)=h(1)= ![]() ,
,
∴0<m ![]() .
.
作出f(x)的函数图象如图所示:

由图象可知y=f(x)与y=m有4个交点,
∴g(x)=f(x)﹣m有4个零点.
所以答案是:4.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】某公司有A、B、C、D、E五辆汽车,其中A、B两辆汽车的车牌尾号均为1,C、D两辆汽车的车牌尾号均为2,E车的车牌尾号为6.已知在非限行日,每辆车可能出车或不出车,A、B、E三辆汽车每天出车的概率均为 ![]() ,C、D两辆汽车每天出车的概率均为
,C、D两辆汽车每天出车的概率均为 ![]() ,五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
,五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
工作日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
限行车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
例如,星期一禁止车牌尾号为0和5的车辆通行.
(1)求该公司在星期一至少有2辆汽车出车的概率;
(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及数学期望.

