题目内容
【题目】如图,在三棱柱ABC﹣A1B1C1中,四边形ACC1A1和BCC1B1均为正方形,且所在平面互相垂直.
(Ⅰ)求证:BC1⊥AB1;
(Ⅱ)求直线BC1与平面AB1C1所成角的大小.

【答案】(I)详见解析;(II)![]() .
.
【解析】
(Ⅰ)由题意建立空间直角坐标系,利用坐标表示向量,求出![]() ⊥
⊥![]() ,即BC1⊥AB1;
,即BC1⊥AB1;
(Ⅱ)求出平面AB1C1的法向量![]() ,再求
,再求![]() 与
与![]() 所成的角,即可得出直线BC1与平面AB1C1所成的角.
所成的角,即可得出直线BC1与平面AB1C1所成的角.
(Ⅰ)由题意,建立空间直角坐标系,如图所示;

设三棱柱ABC﹣A1B1C1的棱长AC=1,则C(0,0,0),
A(1,0,0),B(0,1,0),A1(1,0,1),B1(0,1,1),
C1(0,0,1),
∴![]() (0,﹣1,1),
(0,﹣1,1),![]() (﹣1,1,1),
(﹣1,1,1),
∴![]()
![]() 0﹣1+1=0,
0﹣1+1=0,
∴![]() ⊥
⊥![]() ,即BC1⊥AB1;
,即BC1⊥AB1;
(Ⅱ)设平面AB1C1的法向量为![]() (x,y,z),
(x,y,z),
则 ,
,
∴![]() ,
,
∴![]() ,
,
x=1,![]() (1,0,1);
(1,0,1);
cos![]() ,
, ,
,
∴![]() 与
与![]() 所成的角是60°,
所成的角是60°,
∴直线BC1与平面AB1C1所成的角为30°.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
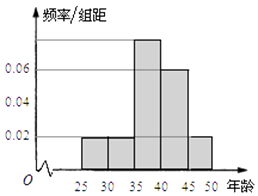
名师指导一卷通系列答案【题目】某单位280名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
(I)现要从年龄低于40岁的员工中用分层抽样的方法抽取12人,则年龄在第1,2,3组的员工人数分别是多少?
(II)为了交流读书心得,现从上述12人中再随机抽取3人发言,设3人中年龄在[35,40)的人数为ξ,求ξ的数学期望;
(III)为了估计该单位员工的阅读倾向,现对从该单位所有员工中按性别比例抽取的40人做“是否喜欢阅读国学类书籍”进行调查,调查结果如下表所示:(单位:人)
喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
男 | 14 | 4 | 18 |
女 | 8 | 14 | 22 |
合计 | 22 | 18 | 40 |
根据表中数据,我们能否有99%的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系?
附: ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |