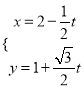题目内容
【题目】在等比数列{an}中,an>0 (n∈N ),公比q∈(0,1),且a1a5+2a3a5+a2a8=25,又a3与a5的等比中项为2.
(1) 求数列{an}的通项公式;
(2) 设![]() ,数列{bn}的前n项和为Sn,当
,数列{bn}的前n项和为Sn,当![]() 最大时,求n的值.
最大时,求n的值.
【答案】(1) 25-n (2) 8或9
【解析】
(1)根据等比数列的性质可知a1a5=a32,a2a8=a52化简a1a5+2a3a5+a2a8=25得到a3+a5=5,又因为a3与a5的等比中项为2,联立求得a3与a5的值,求出公比和首项即可得到数列的通项公式;(2)把an代入到bn=![]() 中得到bn的通项公式,即可得到前n项和的通项sn;把sn代入得到
中得到bn的通项公式,即可得到前n项和的通项sn;把sn代入得到![]() ,讨论求出
,讨论求出![]() 各项和的最大值时n的取值.
各项和的最大值时n的取值.
解 (1)∵a1a5+2a3a5+a2a8=25,
∴a+2a3a5+a=25,
又an>0,∴a3+a5=5.
又a3与a5的等比中项为2,
∴a3a5=4,而q∈(0,1),
∴a3>a5,∴a3=4,a5=1.
∴q=![]() ,a1=16,∴an=16×
,a1=16,∴an=16×![]() n-1=25-n.
n-1=25-n.
(2)bn=log2an=5-n,
∴bn+1-bn=-1,
∴{bn}是以b1=4为首项,-1为公差的等差数列,
∴Sn=![]() ,
,
∴![]() =
=![]() ,
,
∴当n≤8时,![]() >0;
>0;
当n=9时,![]() =0;
=0;
当n>9时,![]() <0.
<0.
∴当n=8或9时,![]() +
+![]() +
+![]() +…+
+…+![]() 最大.
最大.

 轻松课堂单元期中期末专题冲刺100分系列答案
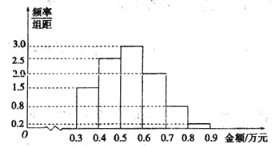
轻松课堂单元期中期末专题冲刺100分系列答案【题目】某电子商务公司随机抽取1000名网购者进行调查.这1000名购物者2018年网购金额(单位:万元)均在区间![]() 内,样本分组为:
内,样本分组为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,购物金额的频率分布直方图如下:
,购物金额的频率分布直方图如下:
电子商务公司决定给购物者发放优惠券,其金额(单位:元)与购物金额关系如下:
购物金额分组 |
|
|
|
|
发放金额 | 50 | 100 | 150 | 200 |
(1)求这1000名购物者获得优惠券金额的平均数;
(2)以这1000名购物者购物金额落在相应区间的频率作为概率,求一个购物者获得优惠券金额不少于150元的概率.
【题目】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到频数分布表和频率分布直方图如下.
组号 | 分组 | 频数 |
1 | [0,2) | 6 |
2 | [2,4) | 8 |
3 | [4,6) | 17 |
4 | [6,8) | 22 |
5 | [8,10) | 25 |
6 | [10,12) | 12 |
7 | [12,14) | 6 |
8 | [14,16) | 2 |
9 | [16,18) | 2 |
合计 | 100 |
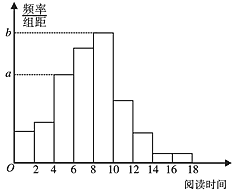
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的频率;
(2)求频率分布直方图中的a,b的值.