题目内容
从某居民区随机抽取10个家庭,获得第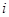 个家庭的月收入
个家庭的月收入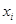 (单位:千元)与月储蓄
(单位:千元)与月储蓄 (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得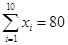 ,
,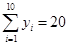 ,
,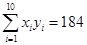 ,
,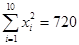 .
.
(1)求家庭的月储蓄 对月收入
对月收入 的线性回归方程
的线性回归方程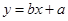 ;
;
(2)判断变量 与
与 之间是正相关还是负相关;
之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
其中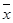 ,
,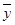 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为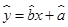
附:线性回归方程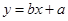 中,
中,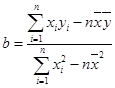 ,
,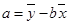 ,
,
(1) 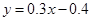 ; (2)
; (2)  与
与 之间是正相关;(3)
之间是正相关;(3) 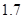
解析试题分析:(1)根据线性回归方程公式先求 ,再求
,再求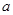 即可得所求方程。(2)线性回归方程的斜率大于0,变量
即可得所求方程。(2)线性回归方程的斜率大于0,变量 与
与 之间是正相关。斜率小于0,变量
之间是正相关。斜率小于0,变量 与
与 之间是负相关。(3) 将
之间是负相关。(3) 将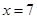 直接代入回归方程即可。
直接代入回归方程即可。
试题解析: (1)由题意知 ,
,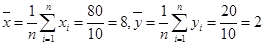
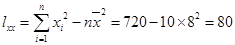 ,
,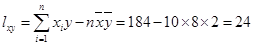 ,由此得
,由此得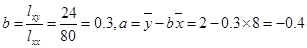 ,
,
故所求回归方程为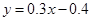
(2)由于变量 的值随
的值随 的值增加而增加
的值增加而增加 ,故
,故 与
与 之间是正相关。
之间是正相关。
(3)将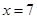 代入回归方程可以榆次该家庭的月储蓄为
代入回归方程可以榆次该家庭的月储蓄为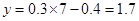 。
。
考点:1线性回归方程;2两个变量间的相关关系。

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
某城市随机抽取一个月( 天)的空气质量指数
天)的空气质量指数 监测数据,统计结果如下:
监测数据,统计结果如下:
 |  |  |  |  |  |  |  |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
| 天数 |  |  |  |  |  |  |  |
(1)根据以上数据估计该城市这
 天空气质量指数
天空气质量指数 的平均值;
的平均值;(2)若该城市某企业因空气污染每天造成的经济损失
 (单位:元)与空气质量指数
(单位:元)与空气质量指数 (记为
(记为 )的
)的关系式为

若在本月
 天中随机抽取一天,试估计该天经济损失
天中随机抽取一天,试估计该天经济损失 大于
大于 元且不超过
元且不超过 元的概率.
元的概率. 一汽车厂生产 、
、 、
、 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
| | 轿车 | 轿车 | 轿车 |
| 舒适型 |  |  |  |
| 标准型 |  |  |  |
 辆,其中有
辆,其中有 类轿车
类轿车 辆.
辆.(1)求
 的值;
的值;(2)用分层抽样的方法在
 类轿车中抽取一个容量为
类轿车中抽取一个容量为 的样本.将该样本看成一个总体,从中任取
的样本.将该样本看成一个总体,从中任取 辆,求至少有
辆,求至少有 辆舒适型轿车的概率;
辆舒适型轿车的概率;(3)用随机抽样的方法从
 类舒适型轿车中抽取
类舒适型轿车中抽取 辆,经检测它们的得分如下:
辆,经检测它们的得分如下: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 .把这
.把这 辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值
辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过
 的概率.
的概率.  名学生的成绩得到频率分布直方图如下:
名学生的成绩得到频率分布直方图如下:
 和
和 的学生中共抽取
的学生中共抽取 人,该
人,该 人,求分数在
人,求分数在 人的概率.
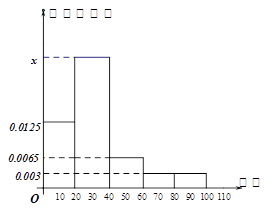
人的概率.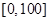 ,样本数据分组为
,样本数据分组为 ,
,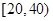 ,
,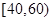 ,
,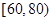 ,
,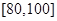 .
.
 的值;
的值;
 ≈5.059)
≈5.059)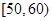 ,
,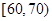 ,
,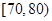 ,
,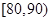 ,
,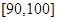 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在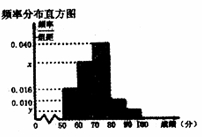

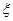 表示所抽取的3名同学中得分在
表示所抽取的3名同学中得分在