题目内容
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是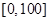 ,样本数据分组为
,样本数据分组为 ,
,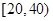 ,
,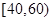 ,
,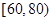 ,
,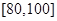 .
.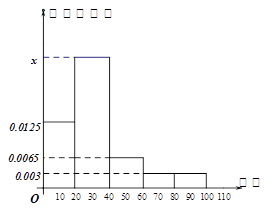
(1)求直方图中 的值;
的值;
(2)如果上学路上所需时间不少于40分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿;
(1)0.025 (2)120 (3)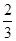
解析试题分析:
(1)根据频率分布直方图可以得到组距为20,而频率分布直方图的纵坐标与组距之积为频率,则可以求的各组的频率,又因为各组频率之和为1,列出式子即可得到x的值.
(2)由第一问可得到每组的频率,根据频率分布直方图可求出所需时间不少于40分钟的学生包含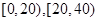 两个组的纵坐标,利用纵坐标与组距相乘即可得到所需时间不少于40分钟的学生的频率,频率乘以总人数即可得到可以留宿学生的人数的估计值.
两个组的纵坐标,利用纵坐标与组距相乘即可得到所需时间不少于40分钟的学生的频率,频率乘以总人数即可得到可以留宿学生的人数的估计值.
试题解析:
(1)由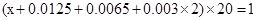 , 4分
, 4分
则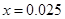 6分
6分
(2)上学所需时间不少于40的学生的频率为: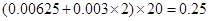 8分
8分
估计学校1000名新生中有: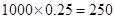 11分
11分
答:估计学校1000名新生中有250名学生可以申请住宿. 12分
考点: 频率分布直方图 频率

 阅读快车系列答案
阅读快车系列答案已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩抽样调查,先将800人按001,002, ,800进行编号;
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检查的3个人的编号;
(下面摘取了第7行到第9行)
(2)抽取的100的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42,若在该样本中,数学成绩优秀率是30%,求a,b的值:
| 人数 | 数学 | |||
| 优秀 | 良好 | 及格 | ||
| 地理 | 优秀 | 7 | 20 | 5 |
| 良好 | 9 | 18 | 6 | |
| 及格 | a | 4 | b | |
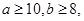 求数学成绩为优秀的人数比及格的人数少的概率.
求数学成绩为优秀的人数比及格的人数少的概率. 在某批次的某种灯泡中,随机地抽取 个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
| 寿命(天) | 频数 | 频率 |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
| 合计 |  |  |
 、
、 的值;
的值;(2)某人从灯泡样品中随机地购买了
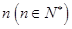 个,如果这
个,如果这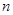 个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求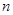 的最小值;
的最小值;(3)某人从这个批次的灯泡中随机地购买了
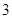 个进行使用,若以上述频率作为概率,用
个进行使用,若以上述频率作为概率,用 表示此人所购买的灯泡中次品的个数,求
表示此人所购买的灯泡中次品的个数,求 的分布列和数学期望.
的分布列和数学期望. 为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
| 应该取消 | 应该保留 | 无所谓 | ||
| 在校学生 | 2100人 | 120人 | y人 | ||
| 社会人士 | 600人 | x人 | z人 |
(1)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
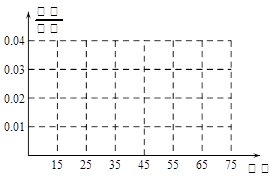
今年年初,我国多个地区发生了持续性大规模的雾霾天气,给我们的身体健康产生了巨大的威胁。私家车的尾气排放也是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力。为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:
| | 患病 | 未患病 | 总计 |
| 没服用药 | 20 | 30 | 50 |
| 服用药 | 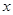 | 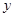 | 50 |
| 总计 | 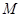 | 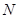 | 100 |
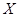 ;从服用药物的动物中任取两只,未患病数为
;从服用药物的动物中任取两只,未患病数为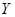 ,工作人员曾计算过
,工作人员曾计算过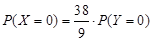 .
. (1)求出列联表中数据
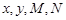 的值;
的值; (2)能够以99%的把握认为药物有效吗?参考公式:
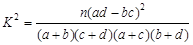 ,其中
,其中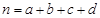 ;
;①当K2≥3.841时有95%的把握认为
 、
、 有关联;
有关联;②当K2≥6.635时有99%的把握认为
 、
、 有关联.
有关联. 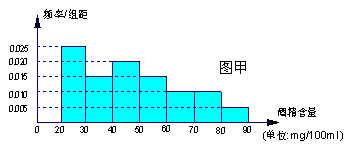
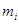 与
与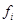 分别表示图甲中各组的组中值及频率)
分别表示图甲中各组的组中值及频率) 
 的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90
的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90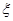 为吴、李两位先生被抽中的人数,求
为吴、李两位先生被抽中的人数,求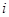 个家庭的月收入
个家庭的月收入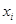 (单位:千元)与月储蓄
(单位:千元)与月储蓄 (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得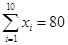 ,
,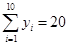 ,
,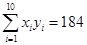 ,
,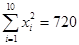 .
. 对月收入
对月收入 的线性回归方程
的线性回归方程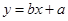 ;
;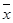 ,
,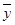 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为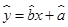
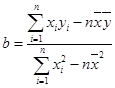 ,
,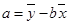 ,
,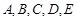 五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为
五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为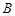 的考生有
的考生有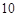 人.
人. 
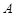 的人数;
的人数; 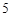 分,
分,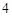 分,
分,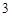 分,
分, 分,
分, 分,求该考场考生“数学与逻辑”科目的平均分;
分,求该考场考生“数学与逻辑”科目的平均分;