题目内容
18.函数f(x)满足x∈(-$\frac{π}{2}$,$\frac{π}{2}$)时,f′(x)>tanx•f(x),则下列式子中正确的序号是④①2f(0)>f($\frac{π}{3}$);②f(-$\frac{π}{3}$)>$\sqrt{2}$f(-$\frac{π}{4}$);③$\frac{\sqrt{3}}{3}$f($\frac{π}{4}$)<$\frac{\sqrt{2}}{2}$f($\frac{π}{6}$);④2f(-1)<$\frac{1}{cos1}$f($\frac{π}{3}$)
分析 由题意得到f′(x)cosx>f(x)sinx,构造函数g(x)=f(x)cosx,判断函数g(x)在(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递增,逐一验证即可.
解答 解:∵f′(x)>tanx•f(x),
∵x∈(-$\frac{π}{2}$,$\frac{π}{2}$),
∴0<cosx≤1
∴f′(x)cosx>f(x)sinx,
构造函数g(x)=f(x)cosx,
∴g′(x)=f′(x)cosx-f(x)sinx>0在x∈(-$\frac{π}{2}$,$\frac{π}{2}$)恒成立,
∴函数g(x)在(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递增,
∵0<$\frac{π}{3}$,
∴g(0)<g($\frac{π}{3}$),
∴f(0)cos0<f($\frac{π}{3}$)cos$\frac{π}{3}$,
∴2f(0)<f($\frac{π}{3}$);故①错误,
∵-$\frac{π}{3}$<-$\frac{π}{4}$,
∴f(-$\frac{π}{3}$)cos(-$\frac{π}{3}$)<f(-$\frac{π}{4}$)cos(-$\frac{π}{4}$),
∴f(-$\frac{π}{3}$)<$\sqrt{2}$f(-$\frac{π}{4}$),故②错误,
∵$\frac{π}{6}$<$\frac{π}{4}$,
∴f($\frac{π}{6}$)cos($\frac{π}{6}$)<f($\frac{π}{4}$)cos($\frac{π}{4}$),
∴$\frac{\sqrt{3}}{2}$f($\frac{π}{6}$)<$\frac{\sqrt{2}}{2}$f($\frac{π}{4}$),
∴$\frac{\sqrt{2}}{2}$f($\frac{π}{6}$)<$\frac{\sqrt{3}}{3}$f($\frac{π}{4}$),故③错误,
∵-1<$\frac{π}{3}$,
∴g(-1)<g($\frac{π}{3}$),
∴f(-1)cos(-1)<f($\frac{π}{3}$)cos$\frac{π}{3}$,
∴2f(-1)<$\frac{1}{cos1}$f($\frac{π}{3}$)故④正确,
故答案为:④
点评 本题考查了函数的单调性和导数的关系,关键是构造函数,属于中档题.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案| A. | $\frac{8\sqrt{15}}{5}$ | B. | $\sqrt{15}$ | C. | $\frac{\sqrt{15}}{2}$ | D. | 6$\sqrt{3}$ |
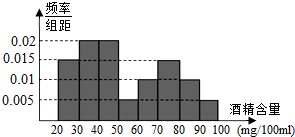 据《南通日报》报道,2015年1月1日至1月31日,市交管部门共抽查了1000辆车,查出酒后驾车和醉酒驾车的驾驶员80人,如图是对这80人血液中酒精含量进行检查所得结果的频率分布直方图.(酒精含量≥80mg/100ml为醉酒驾车)
据《南通日报》报道,2015年1月1日至1月31日,市交管部门共抽查了1000辆车,查出酒后驾车和醉酒驾车的驾驶员80人,如图是对这80人血液中酒精含量进行检查所得结果的频率分布直方图.(酒精含量≥80mg/100ml为醉酒驾车)(1)根据频率分布直方图完成下表:
| 酒精含量(单位:mg/100ml) | [20,30) | [30,40) | [40,50) | [50,60) |
| 人数 | 16 | 16 | 4 | |
| 酒精含量(单位:mg/100ml) | [60,70) | [70,80) | [80,90) | [90,100] |
| 人数 | 4 |
(3)若用分层抽样的方法从血液酒精浓度在[70,90)范围内的驾驶员中抽取一个容量为5的样本,并将该样本看成一个总体,从中任取2人,求恰有1人属于醉酒驾车的概率.
| A. | 345° | B. | -345° | C. | 235° | D. | -435° |
| A. | 2016 | B. | 2015 | C. | 2014 | D. | 2013 |
| A. | [6,12] | B. | (6,12) | C. | [5,12] | D. | (5,12) |