题目内容
6.已知数列{an}满足:a1=2,(n+1)an=(n-1)an-1(n≥2,n∈N*),则$\frac{a_3}{a_1}$=$\frac{1}{6}$,数列{an}的通项公式为$\frac{4}{{n({n+1})}}$.分析 通过对(n+1)an=(n-1)an-1(n≥2,n∈N*)变形可知$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n-1}{n+1}$(n≥2,n∈N*),累乘计算即得结论.
解答 解:∵(n+1)an=(n-1)an-1(n≥2,n∈N*),
∴$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n-1}{n+1}$(n≥2,n∈N*),
∵$\frac{{a}_{2}}{{a}_{1}}$=$\frac{1}{3}$,$\frac{{a}_{3}}{{a}_{2}}$=$\frac{2}{4}$,
∴$\frac{{a}_{3}}{{a}_{1}}$=$\frac{{a}_{3}}{{a}_{2}}$•$\frac{{a}_{2}}{{a}_{1}}$=$\frac{1}{6}$,
同时累乘得:$\frac{{a}_{n}}{{a}_{1}}$=$\frac{1}{3}$•$\frac{2}{4}$•…•$\frac{n-1}{n+1}$=$\frac{2}{n(n+1)}$,
又∵a1=2,
∴an=$\frac{2}{n(n+1)}$•2=$\frac{4}{n(n+1)}$,
故答案为:$\frac{1}{6}$、$\frac{4}{{n({n+1})}}$.
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
11.已知直线l的方向向量为$\overrightarrow{a}$=(-1,0,1),点A(1,2,-1)在l上,则点P(2,-1,2)到l的距离为( )
| A. | $\sqrt{15}$ | B. | 4 | C. | $\sqrt{17}$ | D. | 3$\sqrt{2}$ |
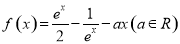 .
.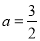 时,求函数
时,求函数 的单调区间;
的单调区间;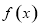 在
在 上为单调函数,求实数
上为单调函数,求实数 的取值范围.
的取值范围. ,则
,则 的值为( )
的值为( ) 如图,在长方形ABCD中,对角线AC与两邻边所成的角分别为α、β,则cos2α+cos2β=1,则在立体几何中,给出类比猜想.
如图,在长方形ABCD中,对角线AC与两邻边所成的角分别为α、β,则cos2α+cos2β=1,则在立体几何中,给出类比猜想.