题目内容
【题目】如图,在棱长为3的正方体ABCD-A1B1C1D1中,A1E=CF=1.
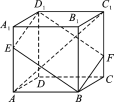
(1)求两条异面直线AC1与BE所成角的余弦值;
(2)求直线BB1与平面BED1F所成角的正弦值.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
(1)先根据题意建立空间直角坐标系,求得向量![]() 和向量
和向量![]() 的坐标,再利用线线角的向量方法求解.
的坐标,再利用线线角的向量方法求解.
(2)先求得平面BED1F的一个法向量,易知向量![]() 的坐标,再利用线面角的向量方法求解.
的坐标,再利用线面角的向量方法求解.
(1)以D为原点,建立空间直角坐标系Dxyz,如图所示,
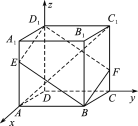
则A(3,0,0),C1(0,3,3),![]() =(-3,3,3),
=(-3,3,3),
B(3,3,0),E(3,0,2),![]() =(0,-3,2).
=(0,-3,2).
所以cos〈![]() 〉=
〉=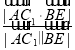 =
=![]() =
=![]() ,
,
故两条异面直线AC1与BE所成角的余弦值为![]() .
.
(2) B(3,3,0),![]() =(0,-3,2),
=(0,-3,2),![]() =(3,0,-1).
=(3,0,-1).
设平面BED1F的一个法向量为n=(x,y,z),
由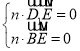 得
得![]()
所以![]() 则n=(x,2x,3x),不妨取n=(1,2,3),
则n=(x,2x,3x),不妨取n=(1,2,3),
设直线BB1与平面BED1F所成的角为α,则
sinα=|cos〈![]() ,n〉|=
,n〉|=![]() =
=![]() .
.
所以直线BB1与平面BED1F所成角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】由国家统计局提供的数据可知,2012年至2018年中国居民人均可支配收入![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均可支配收入 | 1.65 | 1.83 | 2.01 | 2.19 | 2.38 | 2.59 | 2.82 |
(1)求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)利用(1)中的回归方程,分析2012年至2018年中国居民人均可支配收入的变化情况,并预测2019年中国居民人均可支配收入.
附注:参考数据:![]() ,
,![]() .
.
参考公式:回归直线方程![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: 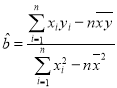 ,
,![]() .
.