题目内容
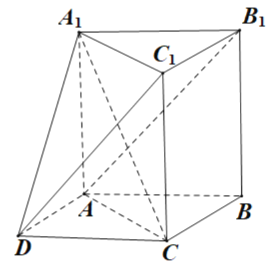
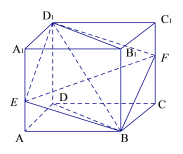
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点E,交棱
于点E,交棱![]() 于点F,则:
于点F,则:
①平面![]() 分正方体所得两部分的体积相等;
分正方体所得两部分的体积相等;
②四边形![]() 一定是平行四边形;
一定是平行四边形;
③平面![]() 与平面
与平面![]() 不可能垂直;
不可能垂直;
④四边形![]() 的面积有最大值.
的面积有最大值.
其中所有正确结论的序号为( )
A.①④B.②③C.①②④D.①②③④
【答案】C
【解析】
根据正方体的性质对每个命题进行判断.结合排除法可选正确结论.
截面上方几何体分割成四棱锥四棱锥![]() ,四棱锥
,四棱锥![]() ,三棱锥
,三棱锥![]() ,截面下方几何体对称的也是三个棱锥,对应体积相等(特殊位置截面更容易得此结论),①正确,排除B;
,截面下方几何体对称的也是三个棱锥,对应体积相等(特殊位置截面更容易得此结论),①正确,排除B;
由正方体相对两个面平行,根据面面平行的性质定理知四边形![]() 的两组对边平行,从而是平行四边形,②正确,排除A;
的两组对边平行,从而是平行四边形,②正确,排除A;
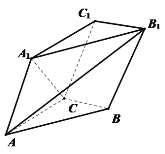
当![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,这时可证
中点,这时可证![]() 平面
平面![]() (先证
(先证![]() ),从而平面
),从而平面![]() 与平面
与平面![]() 垂直,③错误,排除D,
垂直,③错误,排除D,
只有C可选了.
事实上,四边形![]() 即有最大值也有最小值.
即有最大值也有最小值.![]() 与
与![]() (或
(或![]() )重合时面积最大,
)重合时面积最大,![]() 是
是![]() 中点时,面积最小.
中点时,面积最小.
设![]() ,正方体棱长为1,
,正方体棱长为1,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
所以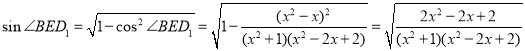 ,
,
所以![]()
![]() ,
,
所以![]() 或1时,
或1时,![]() 取得最大值
取得最大值![]() .④正确.
.④正确.
故选:C.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目