题目内容
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 过点
过点![]() ,焦点
,焦点![]() ,圆
,圆![]() 的直径为
的直径为![]() .
.
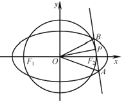
(1)求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 相切于第一象限内的点
相切于第一象限内的点![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.若
两点.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)由椭圆焦点可以确定![]() ,再利用点
,再利用点![]() 代入椭圆方程即可求出
代入椭圆方程即可求出![]() ,从而得到椭圆方程;由圆O的直径为
,从而得到椭圆方程;由圆O的直径为![]() ,即可知圆心坐标为
,即可知圆心坐标为![]() ,半径为
,半径为![]() ,从而得到圆的方程.
,从而得到圆的方程.
(2)设切点坐标为![]() ,即可表示出直线
,即可表示出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程与椭圆方程,消去
的方程与椭圆方程,消去![]() 得到关于
得到关于![]() 的一元二次方程,利用求根公式求出
的一元二次方程,利用求根公式求出![]() ,然后利用弦长公式表示
,然后利用弦长公式表示![]() ,而由条件可求出
,而由条件可求出![]() ,结合
,结合![]() ,即可求出
,即可求出![]() ,从而求出直线
,从而求出直线![]() 的方程.
的方程.
(1)因为椭圆C的焦点为![]() ,
,
可设椭圆C的方程为![]() .
.
又点![]() 在椭圆C上,所以
在椭圆C上,所以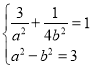 ,解得
,解得
因此,椭圆C的方程为![]() .
.
因为圆O的直径为![]() ,所以其方程为
,所以其方程为![]() .
.
(2)设直线![]() 与圆O相切于
与圆O相切于![]() ,
,
则![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
即![]() .由
.由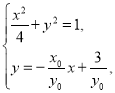 消去y,得
消去y,得
![]() ①
①
因为三角形OAB的面积为![]() ,所以
,所以![]() ,从而
,从而![]() ,
,
设![]() ,由①得
,由①得 ,
,
所以![]()
![]() .因为
.因为![]() ,
,
所以![]() ,即
,即![]() ,解得
,解得![]() 舍去),
舍去),
则![]() ,因此P的坐标为
,因此P的坐标为![]() .
.
故直线l的方程为:![]() .
.

练习册系列答案
相关题目