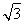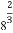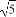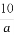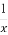Question

已知f(x)=(x≠a).

(1)若a=-2,试证f(x)在(-∞,-2)上单调递增.

(2)若a>0且f(x)在(1,+∞)上单调递减,求a的取值范围.

 

Answer 1

(1)见解析 (2) (0,1]

【解析】(1)任设x1<x2<-2, (0,1]

则f(x1)-f(x2)=-=.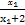

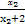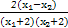∵(x1+2)(x2+2)>0,x1-x2<0,

∴f(x1)<f(x2),

∴f(x)在(-∞,-2)上单调递增.

(2)任设1<x1<x2,则

f(x1)-f(x2)=-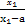

=.

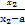
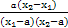∵a>0,x2-x1>0,

∴要使f(x1)-f(x2)>0,只需(x1-a)(x2-a)>0恒成立,∴a≤1.

综上所述知a的取值范围是(0,1].