题目内容
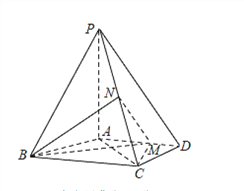
【题目】已知圆![]() 的方程为
的方程为![]() ,点
,点![]() ,点M为圆
,点M为圆![]() 上的任意一点,线段
上的任意一点,线段![]() 的垂直平分线与线段
的垂直平分线与线段![]() 相交于点N.
相交于点N.
(1)求点N的轨迹C的方程.
(2)已知点![]() ,过点A且斜率为k的直线
,过点A且斜率为k的直线![]() 交轨迹C于
交轨迹C于![]() 两点,以
两点,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,是否存在常数k,使得点B在轨迹C上,若存在,求k的值;若不存在,说明理由.
,是否存在常数k,使得点B在轨迹C上,若存在,求k的值;若不存在,说明理由.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)由椭圆的定义![]() ,知点
,知点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点的椭圆,进而求得N的轨迹方程;(2)设直线
为焦点的椭圆,进而求得N的轨迹方程;(2)设直线![]() ,与椭圆联立,得韦达定理,以
,与椭圆联立,得韦达定理,以![]() 、
、![]() 为邻边作平行四边形
为邻边作平行四边形![]() 的顶点
的顶点![]() 在椭圆上,转化为
在椭圆上,转化为![]() 坐标化后B点在椭圆上,得k的方程求解即可
坐标化后B点在椭圆上,得k的方程求解即可
(1)![]()
![]() >
>![]()
知点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点的椭圆,则a=
为焦点的椭圆,则a=![]() ,
,![]()
∴![]()
(2)设直线![]() ,与椭圆联立
,与椭圆联立
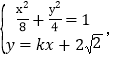 设
设![]() ,
,![]()
消去![]() ,得
,得![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 点
点![]()
代入椭圆方程:![]()
得![]()
又![]() 满足
满足![]()
![]()
![]() 存在常数
存在常数![]() ,使得平行四边形
,使得平行四边形![]() 的顶点
的顶点![]() 在椭圆上
在椭圆上

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目