题目内容
已知A、B、C三点在球心为 ,半径为3的球面上,且三棱锥
,半径为3的球面上,且三棱锥 —ABC为正四面体,那么A、B两点间的球面距离为
—ABC为正四面体,那么A、B两点间的球面距离为
A、 B、
B、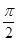 C、
C、 D、
D、
 ,半径为3的球面上,且三棱锥
,半径为3的球面上,且三棱锥 —ABC为正四面体,那么A、B两点间的球面距离为
—ABC为正四面体,那么A、B两点间的球面距离为A、
 B、
B、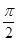 C、
C、 D、
D、
D
解:作出图形,
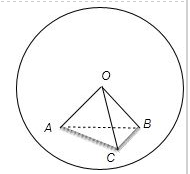
∵几何体O-ABC为正四面体,
∴球心角∠AOB=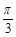 ∴A,B两点的球面距离=
∴A,B两点的球面距离=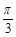 ×3=π.
×3=π.
故填D

∵几何体O-ABC为正四面体,
∴球心角∠AOB=
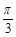 ∴A,B两点的球面距离=
∴A,B两点的球面距离=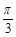 ×3=π.
×3=π.故填D

练习册系列答案
相关题目

 中,侧棱
中,侧棱 底面
底面 ,
, 为
为 的中点,
的中点, ,
, .
.
 平面
平面 ;
; 的体积.
的体积.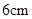 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.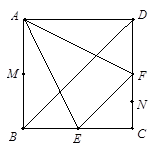
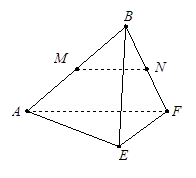

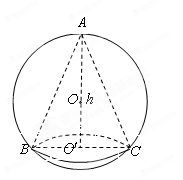
 ,球内接圆锥的高为
,球内接圆锥的高为 ,体积为
,体积为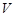 ,
,
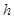 表示
表示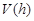 ;
; AB1,BN=
AB1,BN=