题目内容
如图所示,多面体EF﹣ABCD中,底面ABCD为等腰梯形,AB∥CD,四边形ACFE为矩形,且平面ACFE⊥平面ABCD,AD=DC=BC=CF=1,AC⊥BC,∠ADC=120°
(1)求证:BC⊥AF
(2)求平面BDF与平面CDF所成夹角的余弦值.
(1)求证:BC⊥AF
(2)求平面BDF与平面CDF所成夹角的余弦值.

(1)见解析;(2)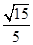
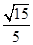
本试题主要考查了立体几何中线线垂直的证明以及二面角平面角的求解的综合运用。(1) ∵平面ACFE⊥平面ABCD且平面ACFE∩平面ABCD=AC
又∵BC⊥AC ∴BC⊥平面ACFE
又∵AF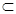 平面ACFE ∴BC⊥AF
平面ACFE ∴BC⊥AF
(2)建立空间直角坐标系,得到点的坐标,从而求解平面的法向量的坐标,进而运用数量积
的性质得到夹角的求解。
(1)证明:
∵平面ACFE⊥平面ABCD且平面ACFE∩平面ABCD=AC
又∵BC⊥AC ∴BC⊥平面ACFE
又∵AF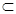 平面ACFE ∴BC⊥AF
平面ACFE ∴BC⊥AF
方法二:建系后用向量证之(略)
(2)解:由已知,以C为坐标原点,CA,CB,CF所在直线分别为x,y,z轴建立如图所示的空间直角坐标系C-xyz,连接BD交AC于O点,连接OF,要使AM∥平面BDF,易得AM∥OF
∵AD=DC=BC=CF=1,∠ADC=120°
∴AC=BD=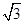 ,OC=
,OC=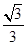 ,
,
即B(0,1,0),D(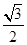 ,
,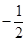 ,0),F(0,0,1)
,0),F(0,0,1)
∴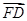 =(
=(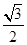 ,
,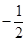 ,-1),
,-1),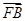 =(0,1,-1),
=(0,1,-1),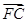 =(0,0,-1)
=(0,0,-1)
设平面BDF的法向量为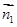 =(x,y,z)
=(x,y,z)
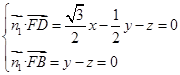
令z=1,则y=1,x=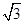 ,∴
,∴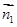 =(
=(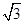 ,1,1)
,1,1)
设平面CDF的法向量为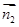 =(x,y,z)
=(x,y,z)
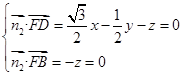
令x=1,则y=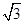 ,z=0,∴
,z=0,∴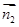 =(1,
=(1,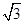 ,0)
,0)
设平面BDF与平面CDF的夹角为α
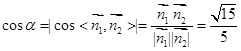
又∵BC⊥AC ∴BC⊥平面ACFE
又∵AF
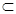 平面ACFE ∴BC⊥AF
平面ACFE ∴BC⊥AF(2)建立空间直角坐标系,得到点的坐标,从而求解平面的法向量的坐标,进而运用数量积
的性质得到夹角的求解。
(1)证明:
∵平面ACFE⊥平面ABCD且平面ACFE∩平面ABCD=AC
又∵BC⊥AC ∴BC⊥平面ACFE
又∵AF
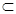 平面ACFE ∴BC⊥AF
平面ACFE ∴BC⊥AF方法二:建系后用向量证之(略)
(2)解:由已知,以C为坐标原点,CA,CB,CF所在直线分别为x,y,z轴建立如图所示的空间直角坐标系C-xyz,连接BD交AC于O点,连接OF,要使AM∥平面BDF,易得AM∥OF
∵AD=DC=BC=CF=1,∠ADC=120°
∴AC=BD=
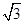 ,OC=
,OC=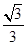 ,
,即B(0,1,0),D(
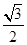 ,
,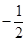 ,0),F(0,0,1)
,0),F(0,0,1)∴
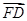 =(
=(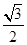 ,
,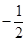 ,-1),
,-1),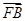 =(0,1,-1),
=(0,1,-1),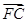 =(0,0,-1)
=(0,0,-1)设平面BDF的法向量为
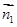 =(x,y,z)
=(x,y,z)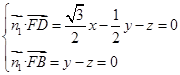
令z=1,则y=1,x=
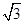 ,∴
,∴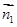 =(
=(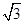 ,1,1)
,1,1)设平面CDF的法向量为
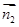 =(x,y,z)
=(x,y,z)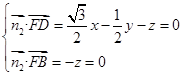
令x=1,则y=
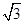 ,z=0,∴
,z=0,∴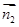 =(1,
=(1,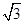 ,0)
,0)设平面BDF与平面CDF的夹角为α
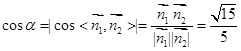

练习册系列答案
相关题目
 平面
平面

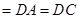 =
= ,
, 和平面
和平面 所成的角为
所成的角为 ,且点
,且点 在平面
在平面 的平分线上.
的平分线上.
 平面
平面
 的余弦值
的余弦值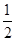 ,求这个圆台的侧面积.
,求这个圆台的侧面积. 
 的棱长为1,线段
的棱长为1,线段 上有两个动点E, F,
上有两个动点E, F, ,
,


 与平面
与平面 所成的角为定值
所成的角为定值 所成的角为定值
所成的角为定值 中,
中, ,且
,且 分别是
分别是 的中点。
的中点。
 ,半径为3的球面上,且三棱锥
,半径为3的球面上,且三棱锥 B、
B、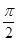 C、
C、 D、
D、
 被以A为球心,AB为半径的球相截,则所截得几何体(球内部分)的表面积为 ( )
被以A为球心,AB为半径的球相截,则所截得几何体(球内部分)的表面积为 ( )