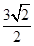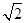题目内容
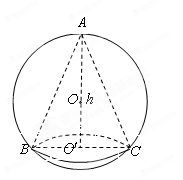
如图,已知球的半径为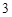 ,球内接圆锥的高为
,球内接圆锥的高为 ,体积为
,体积为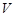 ,
,
(1)写出以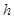 表示
表示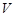 的函数关系式
的函数关系式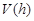 ;
;
(2)当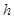 为何值时,
为何值时,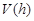 有最大值,并求出该最大值.
有最大值,并求出该最大值.
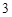 ,球内接圆锥的高为
,球内接圆锥的高为 ,体积为
,体积为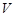 ,
,
(1)写出以
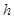 表示
表示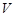 的函数关系式
的函数关系式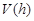 ;
;(2)当
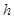 为何值时,
为何值时,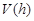 有最大值,并求出该最大值.
有最大值,并求出该最大值. (1)  ;
;
(2)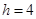 时,
时,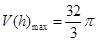
 ;
;(2)
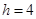 时,
时,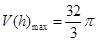
本试题主要考查了导数在研究最值问题中的运用。
利用已知条件,设出变量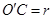 ,然后得到
,然后得到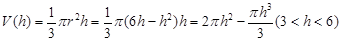
借助于函数求解导数,然后判定单调性得到最值。
解:(1)连接 ,设
,设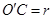 ,有
,有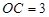 ,
, ,则有
,则有
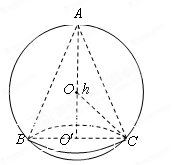
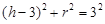 ,即
,即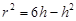 .
. 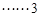 分
分
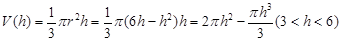
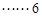 分
分
(2)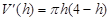 ,当
,当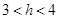 ,
,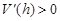 ,
,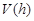 单增;
单增;
当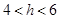 ,
,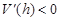 ,
,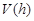 单减;
单减;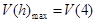 .
. 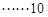 分
分
当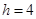 时,
时,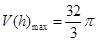 .
. 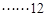 分
分
利用已知条件,设出变量
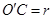 ,然后得到
,然后得到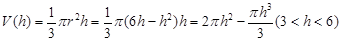
借助于函数求解导数,然后判定单调性得到最值。
解:(1)连接
 ,设
,设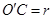 ,有
,有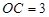 ,
, ,则有
,则有
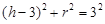 ,即
,即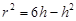 .
.  分
分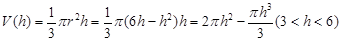
 分
分(2)
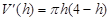 ,当
,当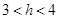 ,
,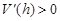 ,
,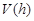 单增;
单增;当
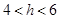 ,
,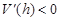 ,
,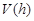 单减;
单减;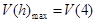 .
. 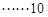 分
分当
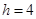 时,
时,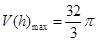 .
. 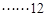 分
分
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
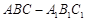 中,
中,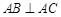 ,
,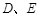 分别为
分别为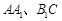 的中点,
的中点,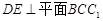 ,二面角
,二面角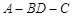 的大小为
的大小为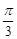 .
.
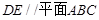 ;
;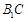 与平面
与平面 所成的角的大小.
所成的角的大小. 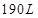 ,假如它的两底面边长分别等于
,假如它的两底面边长分别等于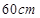 和
和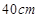 ,求它的深度为多少
,求它的深度为多少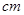 ?
? 中,
中, ,且
,且 分别是
分别是 的中点。
的中点。
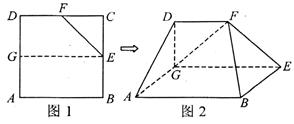
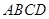 绕点
绕点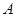 逆时针旋转
逆时针旋转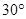 到正方形
到正方形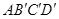 ,图中阴影部分的面积为( )
,图中阴影部分的面积为( )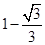
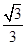
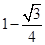
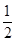

 ,半径为3的球面上,且三棱锥
,半径为3的球面上,且三棱锥 B、
B、 C、
C、 D、
D、