题目内容
已知点(1,1)是椭圆
+
=1某条弦的中点,则此弦所在的直线方程为:______.
| x2 |
| 4 |
| y2 |
| 2 |
设以A(1,1)为中点椭圆的弦与椭圆交于E(x1,y1),F(x2,y2),
∵A(1,1)为EF中点,
∴x1+x2=2,y1+y2=2,
把E(x1,y1),F(x2,y2)分别代入椭圆
+
=1,
可得
+
=1,
+
=1
两式相减,可得(x1+x2)(x1-x2)+2(y1+y2)(y1-y2)=0,
∴2(x1-x2)+4(y1-y2)=0,
∴k=
=-
∴以A(1,1)为中点椭圆的弦所在的直线方程为:y-1=-
(x-1),
整理,得x+2y-3=0.
故答案为:x+2y-3=0.
∵A(1,1)为EF中点,
∴x1+x2=2,y1+y2=2,
把E(x1,y1),F(x2,y2)分别代入椭圆
| x2 |
| 4 |
| y2 |
| 2 |
可得
| x12 |
| 4 |
| y12 |
| 2 |
| x22 |
| 4 |
| y22 |
| 2 |
两式相减,可得(x1+x2)(x1-x2)+2(y1+y2)(y1-y2)=0,
∴2(x1-x2)+4(y1-y2)=0,
∴k=
| y1-y2 |
| x1-x2 |
| 1 |
| 2 |
∴以A(1,1)为中点椭圆的弦所在的直线方程为:y-1=-
| 1 |
| 2 |
整理,得x+2y-3=0.
故答案为:x+2y-3=0.

练习册系列答案
相关题目
 为坐标原点,给定两点
为坐标原点,给定两点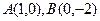 ,点
,点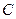 满足
满足 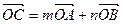 ,其中
,其中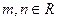 ,且
,且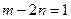 . (1)求点
. (1)求点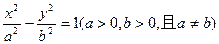 交于
交于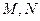 两点,且以
两点,且以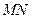 为直径的圆过原点,求证:
为直径的圆过原点,求证: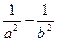 为定值;(3)在(2)的条件下,若双曲线的离心率不大于
为定值;(3)在(2)的条件下,若双曲线的离心率不大于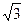 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.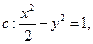 设过点
设过点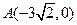 的直线l的方向向量
的直线l的方向向量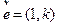
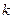 >
>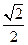 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为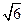 .
.