题目内容
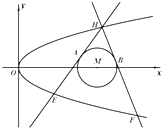
如图,已知抛物线C:y2=2px和⊙M:(x-4)2+y2=1,过抛物线C上一点H(x0,y0)作两条直线与⊙M相切于A、B两点,分别交抛物线为E、F两点,圆心点M到抛物线准线的距离为
.
(1)求抛物线C的方程;
(2)当∠AHB的角平分线垂直x轴时,求直线EF的斜率.
| 17 |
| 4 |
(1)求抛物线C的方程;
(2)当∠AHB的角平分线垂直x轴时,求直线EF的斜率.

(1)∵点M(4,0)到抛物线准线的距离为4+
=
,
∴p=
,即抛物线C的方程为y2=x.
(2)∵当∠AHB的角平分线垂直x轴时,点H(4,2),∴kHE=-kHF,
设E(x1,y1),F(x2,y2),
∴
=-
,
∴
=-
,
∴y1+y2=-2yH=-4.
kEF=
=
=
=-
.
| p |
| 2 |
| 17 |
| 4 |
∴p=
| 1 |
| 2 |
(2)∵当∠AHB的角平分线垂直x轴时,点H(4,2),∴kHE=-kHF,
设E(x1,y1),F(x2,y2),
∴
| yH-y1 |
| xH-x1 |
| yH-y2 |
| xH-x2 |
∴
| yH-y1 | ||||
|
| yH-y2 | ||||
|
∴y1+y2=-2yH=-4.
kEF=
| y2-y1 |
| x2-x1 |
| y2-y1 | ||||
|
| 1 |
| y1+y2 |
| 1 |
| 4 |

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 ,点
,点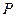 满足
满足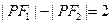 ,记点
,记点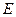 .
.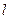 过点
过点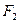 且与轨迹
且与轨迹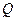 两点. (i)设点
两点. (i)设点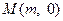 ,问:是否存在实数
,问:是否存在实数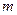 ,使得直线
,使得直线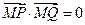 成立?若存在,求出实数
成立?若存在,求出实数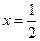 的垂线
的垂线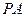 、
、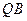 ,垂足分别为
,垂足分别为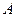 、
、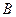 ,记
,记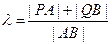 ,求
,求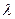 的取值范围.
的取值范围.