Question

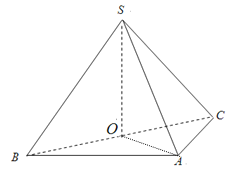
【题目】如图，在三棱锥中，侧面与侧面均为边长为2的等边三角形，，为中点．

（1）证明：平面；

（2）求点B到平面的距离．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）由题设AB=AC=SB=SC=SA，连结OA，推导出SO⊥BC，SO⊥AO，由此能证明SO⊥平面ABC;

（2）设点B到平面SAC的距离为h，由VS﹣BAC=VB﹣SAC，能求出点B到平面SAC的距离．

（1）由题设 ，连结，为等腰直角三角形，所以，且，

又为等腰三角形，故，且，

从而．所以为直角三角形，．

又．

所以平面．

（2）设B到平面SAC的距离为，则由（Ⅰ）知：三棱锥

即

∵为等腰直角三角形,且腰长为2.

∴

∴

∴△SAC的面积为=

△ABC面积为, ∴,

∴B到平面SAC的距离为