题目内容
【题目】某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响，已知某学生只选修甲的概率为0.08，只选修甲和乙的概率是0.12，至少选修一门的概率是0.88，用
表示该学生选修的课程门数和没有选修的课程门数的乘积．
（1）记“函数
为
上的偶函数”为事件
，求事件的概率；
（2）求的分布列和数学期望．
【答案】（1）0．24
（2）
ξ | 0 | 2 |
P | 0．24 | 0．76 |
【解析】试题分析：（1）要想求事件
的概率，由“函数
为
上的奇函数”可知
，将问题转化为“当时的概率”. 又因为
表示该学生选修的课程门数和没有选修的课程门数的乘积，可将问题分为两种情况：该学生选修三门功课或三门功课都没选.不管哪种情况，都需要知道该学生选修甲、乙、丙的概率.所以，首先要求出该学生选修甲、乙、丙的概率.由题意可设该学生选修甲、乙、丙的概率分别为
、
、
，联立方程组求解.再根据问题的两种情况进行求解.
(2)因为表示该学生选修的课程门数和没有选修的课程门数的乘积，分析可得以下2类对立事件：当选修三门功课或三门功课都没选时，；选修其中的一门时，
.由（1）知时的概率为
，则时的概率为
.可将的分布列写出，再计算出数学期望.
试题解析：设该学生选修甲、乙、丙的概率分别为、、
依题意得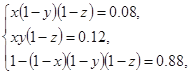
解得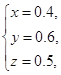
（1）若函数
为的奇函数，则.
当时，表示该学生选修三门功课或三门功课都没选.
事件的概率为
.
（2）依题意知或
，则的分布列为
由（1）知
的数学期望为
【题目】某大学高等数学老师这学期分别用
两种不同的教学方式试验甲、乙两个大一新班（人数均为60人，入学数学平均分数和优秀率都相同；勤奋程度和自觉性都一样）。现随机抽取甲、乙两班各20名的高等数学期末考试成绩，得到茎叶图：
（Ⅰ）依茎叶图判断哪个班的平均分高？
（Ⅱ）现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学，求成绩为86分的同学至少有一个被抽中的概率；
（Ⅲ）学校规定：成绩不低于85分的为优秀，请填写下面的
列联表，并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关？”
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
下面临界值表仅供参考：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：
其中
）
