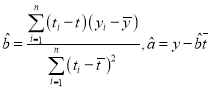题目内容
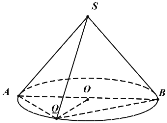
【题目】在直角坐标系xOy中,曲线C1的参数方程为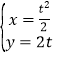 (t为参数),曲线C2的参数方程为
(t为参数),曲线C2的参数方程为![]() (α为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(α为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C1和C2的极坐标方程;
(2)直线l的极坐标方程为![]() ,直线l与曲线C1和C2分别交于不同于原点的A,B两点,求|AB|的值.
,直线l与曲线C1和C2分别交于不同于原点的A,B两点,求|AB|的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)直接利用转换关系,把参数方程直角坐标方程和极坐标方程之间进行转换.
(2)利用极径的应用求出结果.
(1)曲线C1的参数方程为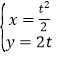 (t为参数),
(t为参数),
转换为直角坐标方程为:y2=8x,
转换为极坐标方程为:ρsin2θ=8cosθ.
曲线C2的参数方程为![]() (α为参数),
(α为参数),
转换为直角坐标方程为:x2+y2-2x-2y=0,
转换为极坐标方程为:ρ-2cosθ-2sinθ=0.
(2)设A(![]() )B(
)B(![]() ),
),
所以: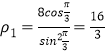 ,
,![]() ,
,
所以:![]() .
.

练习册系列答案
相关题目
【题目】某商店为迎接端午节,推出两款粽子:花生粽和肉粽.为调查这两款粽子的受欢迎程度,店员连续10天记录了这两种粽子的销售量,如下表表示(其中销售单位:个)
天数 销售量
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
花生粽 | 103 | 93 | 98 | 93 | 106 | 86 | 87 | 94 | 91 | 99 | 100 |
肉粽 | 88 | 97 | 98 | 95 | 101 | 98 | 103 | 106 | 103 | 111 | 100 |
(1)根据两组数据完成下面茎叶图:
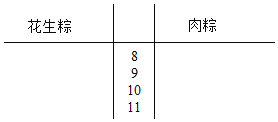
(2)统计学知识,请评述哪款粽子更受欢迎;
(3)求肉粽销售量y关于天数t的线性回归方程,并预估第15天肉粽的销售量(回归方程系数精确到0.1)
参考数据:![]() ,参考公式:
,参考公式: