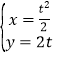Question

【题目】过圆锥轴的截面为等腰直角三角形，为底面圆周上一点，已知，圆锥体积为，点为底面圆的圆心

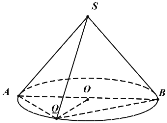
（1）求该圆锥的全面积

（2）求异面直线与所成角的大小（结果用反三角函数表示）

（3）求点到平面的距离

Answer 1

【答案】（1）（2）（3）

【解析】

（1）设底面圆的半径为,则高,利用体积公式求出,即可求出侧面积,进而求得该圆锥的全面积;

（2）连接并延长交圆周于点,再连接,则,所以四边形是平行四边形,,的大小为异面直线与所成角的大小;

（3）求三棱锥的体积以为顶点,以底面,也可以为顶点,以底面,通过等体积法求解点到平面的距离.

（1）设底面圆的半径为

等腰直角,故:

根据圆锥的体积计算公式:

得:

母线的长为

圆锥的侧面展开图为扇形,根据扇形面积公式:

圆锥的侧面积为:

圆锥的全面积

（2）

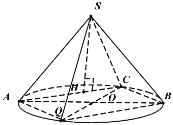
如图:连接并延长交圆周于点, 再连接

四边形是平行四边形,得

的大小为异面直线与所成角的大小.

由（1）知在中,,

过点作于点

为等腰三角形,故

在中有: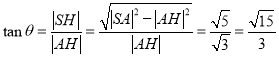

（3） 根据三棱锥的体积计算公式:

在中 可得:

中 故:

得:

解得:

点到平面的距离为:.