题目内容
已知f(x)是定义在R上的奇函数.当x>0时,f(x)=x2-4x,则不等式f(x)>x的解集用区间表示为 .
(-5,0)∪(5,+∞)
设x<0,
则-x>0,f(-x)=x2+4x,
所以x<0时,f(x)=-x2-4x.
所以f(x)=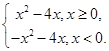
当x≥0时,由x2-4x>x,解得x>5,
当x<0时,由-x2-4x>x,
解得-5<x<0,
故不等式的解集为(-5,0)∪(5,+∞).
则-x>0,f(-x)=x2+4x,
所以x<0时,f(x)=-x2-4x.
所以f(x)=
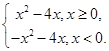
当x≥0时,由x2-4x>x,解得x>5,
当x<0时,由-x2-4x>x,
解得-5<x<0,
故不等式的解集为(-5,0)∪(5,+∞).

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
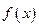 满足
满足 ,则
,则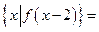 ( )
( )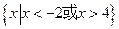

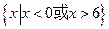
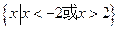
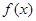 是定义在
是定义在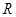 上的偶函数,
上的偶函数,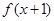 为奇函数,
为奇函数,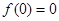 ,当
,当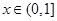 时,
时,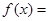 log2x,则在
log2x,则在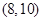 内满足方程
内满足方程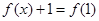 的实数
的实数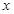 为
为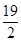
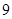
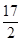
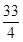
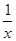 ,则f(-1)等于( )
,则f(-1)等于( )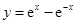
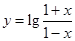
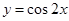
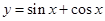
 ),b=f(
),b=f( ),c=f(
),c=f( ),则( )
),则( )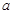 为实常数,
为实常数,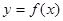 是定义在
是定义在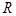 上的奇函数,且当
上的奇函数,且当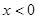 时,
时,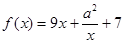 .
.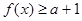 对一切
对一切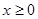 成立,则
成立,则