题目内容
求与x轴相切,圆心在直线3x-y=0上,且被直线x-y=0所截弦长为27的圆的方程.
(x-1)2+(y-3)2=9或(x+1)2+(y+3)2=9.
圆心O在直线3x-y=0上,设圆心坐标为(a,3a),
∴圆心到直线x-y=0的距离为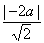
.
又圆与x轴相切,则圆半径r=3|a|.
故设圆的方程为(x-a)2+(y-3a)2=9a2,
设线段A1A2中点为A,则|A1A|=7.
在Rt△OA1A中,由勾股定理得
,解得a=±1,r2=9.
∴所求圆的方程为(x-1)2+(y-3)2=9或(x+1)2+(y+3)2=9.
∴圆心到直线x-y=0的距离为
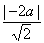.又圆与x轴相切,则圆半径r=3|a|.
故设圆的方程为(x-a)2+(y-3a)2=9a2,
设线段A1A2中点为A,则|A1A|=7.
在Rt△OA1A中,由勾股定理得
,解得a=±1,r2=9.∴所求圆的方程为(x-1)2+(y-3)2=9或(x+1)2+(y+3)2=9.
练习册系列答案
相关题目
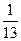
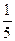
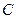和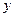
轴相切，圆心在直线
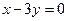上，且被直线
截得的弦长为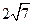
，求圆
围成的图形的面积。
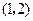且与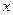
轴相切的圆的方程 ．