题目内容
(满分12分)
已知正项数列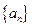
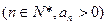 的前
的前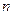 项和
项和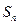 满足:
满足: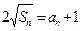 ;设
;设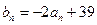 ,求数列
,求数列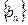 的前
的前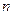 项和的最大值。
项和的最大值。
已知正项数列
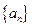
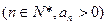 的前
的前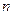 项和
项和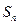 满足:
满足: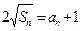 ;设
;设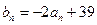 ,求数列
,求数列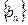 的前
的前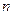 项和的最大值。
项和的最大值。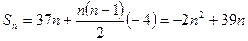
当
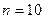 时
时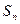 最大,最大值为
最大,最大值为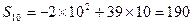
解:当
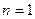 时,
时,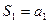 ,所以
,所以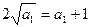 ,即
,即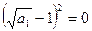 ,∴
,∴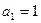 ;
; ……1分
……1分当
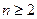 时,由
时,由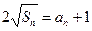 ,得
,得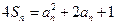 ……①,
……①, ∴
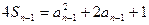 ……② 两式相减,得
……② 两式相减,得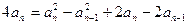
整理,得
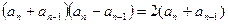 ,…………6分
,…………6分∵
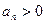 ,∴
,∴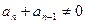 , ∴
, ∴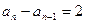 ,
,∴
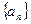 是以1为首项,以2为公差的等差数列,
是以1为首项,以2为公差的等差数列,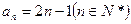 …………8分
…………8分∴
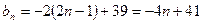 ,∴
,∴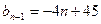 ,
,∴
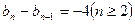 ,又
,又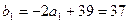
∴
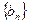 是等差数列,且
是等差数列,且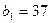 ,公差
,公差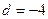 ,
,∴
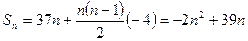 ,…………10分
,…………10分∴当
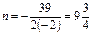 时,
时,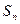 取最大值,但
取最大值,但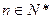
 ,…………11分
,…………11分∴当
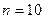 时
时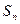 最大,最大值为
最大,最大值为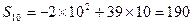 。…………12分
。…………12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
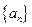 满足:
满足: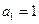 ,且当
,且当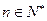 时,
时,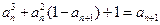 .
.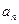 与
与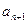 的大小,并证明你的结论.
的大小,并证明你的结论.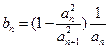 ,其中
,其中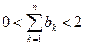 .
.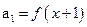 ,
,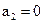 ,
,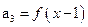 ,其中
,其中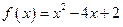 ,数列{an}前n项和存在最小值。
,数列{an}前n项和存在最小值。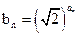 ,求数列
,求数列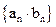 的前n项和
的前n项和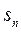
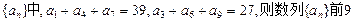 项的和
项的和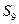 =( )
=( )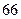 B
B 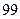 C
C 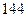 D
D 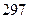
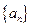 与数列
与数列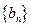 的前
的前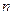 项和分别为
项和分别为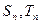 ,且满足
,且满足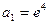 ,
,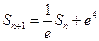 ,
,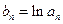
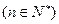 ,则当
,则当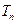 取最大值时,
取最大值时,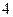
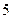
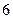
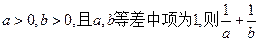 的最小值为( )
的最小值为( )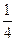
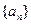 中,
中,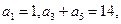 其前n项和
其前n项和 ,则n=__
,则n=__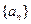 的前四项依次为
的前四项依次为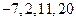 的一个通项公式是 ( )
的一个通项公式是 ( )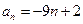
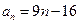
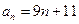
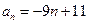
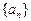 为等差数列,
为等差数列,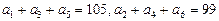 ,以
,以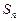 表示
表示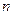 项和,则使
项和,则使