题目内容
1.已知在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,已知∠A=$\frac{π}{4}$,bsin($\frac{π}{4}$+C)-csin($\frac{π}{4}$+B)=a,求证:∠B-∠C=$\frac{π}{2}$.分析 根据正弦定理以及两角和差的正弦公式进行证明即可.
解答 证明:∵bsin($\frac{π}{4}$+C)-csin($\frac{π}{4}$+B)=a,A=$\frac{π}{4}$,
∴由正弦定理可得sinBsin($\frac{π}{4}$+C)-sinCsin($\frac{π}{4}$+B)=sinA.
sinB($\frac{\sqrt{2}}{2}$sinC+$\frac{\sqrt{2}}{2}$cosC)-sinC($\frac{\sqrt{2}}{2}$sinB+$\frac{\sqrt{2}}{2}$cosB)=$\frac{\sqrt{2}}{2}$,
整理得sinBcosC-cosBsinC=1,
即sin(B-C)=1,
∵A=$\frac{π}{4}$,
∴B+C=$\frac{3π}{4}$,
即0<B<$\frac{3π}{4}$,0<C<$\frac{3π}{4}$,
∴-$\frac{3π}{4}$<-C<0,
则-$\frac{3π}{4}$<B-C<$\frac{3π}{4}$,
从而B-C=$\frac{π}{2}$.
点评 本题主要考查正弦定理的应用,利用两角和差的正弦公式进行化简是解决本题的关键.

练习册系列答案
相关题目
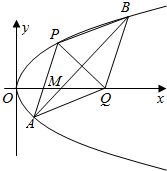 已知过抛物线y2=2px(p>0)上一点A(4,y0)到焦点F的距离为5.
已知过抛物线y2=2px(p>0)上一点A(4,y0)到焦点F的距离为5.