题目内容
（本小题满分14分）将一颗骰子先后抛掷2次，观察向上的点数，求：
（Ⅰ）两数之和为5的概率；
（Ⅱ）以第一次向上
点数为横坐标x，第二次向上的点数为纵坐标y的点(x,y)在圆
=15的内部的概率． 解: 将一颗骰子先后抛掷2次，此问题中含有36个等可能基本事件 
（I）记“两数之和为5”为事件A，则事件A中含有4个基本事件，
所以P（A）=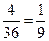
； 答：两数之和为5的概率为
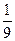． （6分）
（II）基本事件总数为36，点（x，y）在圆x2+y2=15的内部记为事件C，则C包含8个事件，所以P（C
）=
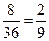． 答：点(x,y)在圆x2+y2=15的内部的概率为
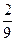．（8分）
（I）记“两数之和为5”为事件A，则事件A中含有4个基本事件，
所以P（A）=
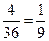； 答：两数之和为5的概率为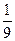． （6分） （II）基本事件总数为36，点（x，y）在圆x2+y2=15的内部记为事件C，则C包含8个事件，所以P（C
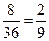）=． 答：点(x,y)在圆x2+y2=15的内部的概率为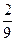．（8分）略
练习册系列答案
教材全解字词句篇系列答案
相关题目
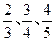， 且各轮考核通过与否相互独立。
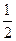，安排最后两道题，每题得出正确答案的概率为
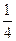，且每题答对与否相互独立，同时规定：每题选对得5分，不选或选错得0分．
，
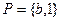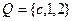，且满足
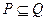, 若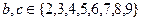
．
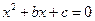有实根的概率
与
轴所围成阴影部分的概率为 . 
且E（
）=10，D（
.