题目内容
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求椭圆的方程;
(2)设点![]() 为
为![]() 的中点.
的中点.
(i)若![]() 轴上存在点
轴上存在点![]() ,对于任意的
,对于任意的![]() ,都有
,都有![]() (
(![]() 为原点),求出点
为原点),求出点![]() 的坐标;
的坐标;
(ii)射线![]() (
(![]() 为原点)与椭圆
为原点)与椭圆![]() 交于点
交于点![]() ,满足
,满足![]() ,求正数
,求正数![]() 的值.
的值.
【答案】(Ⅰ)![]() ; (Ⅱ)(i)见解析; (ii)
; (Ⅱ)(i)见解析; (ii)![]() .
.
【解析】
(I)根据椭圆的左顶点为![]() ,离心率为
,离心率为![]() ,结合性质
,结合性质![]() ,列出关于
,列出关于![]() 、
、![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() ,即可得结果;(Ⅱ)(i)假设
,即可得结果;(Ⅱ)(i)假设![]() 轴上存在着点
轴上存在着点![]() 使得
使得![]() ,设
,设![]()
![]() ,与椭圆方程联立,求得
,与椭圆方程联立,求得![]() ,利用斜率公式,结合
,利用斜率公式,结合![]() 可求得
可求得![]() ;(ii)设
;(ii)设![]() 所在直线方程为
所在直线方程为![]() ,与椭圆方程联立,利用弦长公式、点到直线距离公式结合韦达定理求出
,与椭圆方程联立,利用弦长公式、点到直线距离公式结合韦达定理求出![]() ,再由
,再由![]() 可得
可得![]() ,解方程即可得结果.
,解方程即可得结果.
(I)由已知得![]() 又
又![]() 椭圆方程为:
椭圆方程为:![]() ,
,
(II) (i)假设![]() 轴上存在着点
轴上存在着点![]() 使得
使得![]() ,
,
设![]() 所在的直线方程为:
所在的直线方程为:![]() ,点
,点![]()
由![]() 解得
解得![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
,
解得![]()
![]()
![]() 轴上存在着点
轴上存在着点 ![]() 使得
使得 ![]() 成立,
成立,
(ii)设![]() 所在直线方程为
所在直线方程为![]() ,则
,则
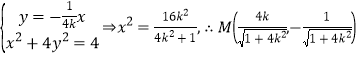 ,
,
![]() 到直线
到直线![]() 的距离:
的距离:![]()
![]() ,
,
![]()
即![]() ,
,![]() ,
,
![]()
解得![]() ,
,![]() .
.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目