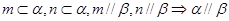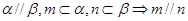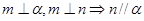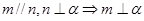题目内容
(本题满分14分)已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=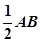 ,N为AB上一点,AB=4AN, M,S分别为PB,BC的中点.
,N为AB上一点,AB=4AN, M,S分别为PB,BC的中点.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.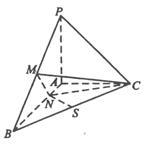
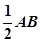 ,N为AB上一点,AB=4AN, M,S分别为PB,BC的中点.
,N为AB上一点,AB=4AN, M,S分别为PB,BC的中点.(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.

(1)见解析;(2)45°.
第一问中,利用建立空间直角坐标系,结合数量积为零来判定线线的垂直关系
第二问中,在第一问的基础上,分别求解得到平面MCN的法向量,然后得到直线SN的方向向量,利用法向量与方向向量来求解线面角的大小。
证明:设PA=1,以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立空间直角坐标系如图。
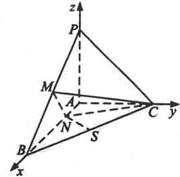
则P(0,0,1),C(0,1,0),B(2,0,0),M(1,0,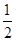 ),N(
),N(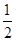 ,0,0),S(1,
,0,0),S(1,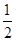 ,0).……4分
,0).……4分
(Ⅰ)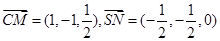 ,
,
因为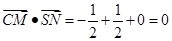 ,所以CM⊥SN ……6分
,所以CM⊥SN ……6分
(Ⅱ)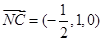 ,设a=(x,y,z)为平面CMN的一个法向量,
,设a=(x,y,z)为平面CMN的一个法向量,
则 ……9分
……9分
因为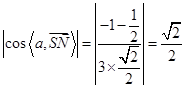 所以SN与平面CMN所成角为45°。…14分
所以SN与平面CMN所成角为45°。…14分
第二问中,在第一问的基础上,分别求解得到平面MCN的法向量,然后得到直线SN的方向向量,利用法向量与方向向量来求解线面角的大小。
证明:设PA=1,以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立空间直角坐标系如图。

则P(0,0,1),C(0,1,0),B(2,0,0),M(1,0,
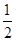 ),N(
),N(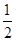 ,0,0),S(1,
,0,0),S(1,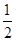 ,0).……4分
,0).……4分(Ⅰ)
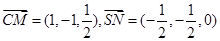 ,
,因为
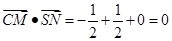 ,所以CM⊥SN ……6分
,所以CM⊥SN ……6分(Ⅱ)
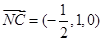 ,设a=(x,y,z)为平面CMN的一个法向量,
,设a=(x,y,z)为平面CMN的一个法向量,则
 ……9分
……9分因为
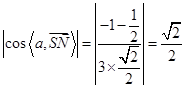 所以SN与平面CMN所成角为45°。…14分
所以SN与平面CMN所成角为45°。…14分
练习册系列答案
相关题目
 中,
中, 平面
平面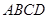 ,底面
,底面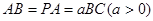 .
.
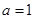 时,求证:
时,求证: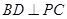 ;
;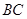 边上有且只有一个点
边上有且只有一个点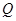 ,使得
,使得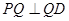 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.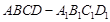 中,
中,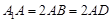 ,
,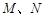 分别是
分别是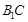 、
、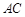 中点。
中点。 ;
; 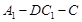 的正切值。
的正切值。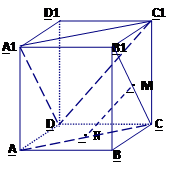
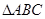 中,若
中,若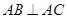 ,
,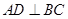 于
于 ,则
,则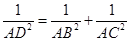 .在四面体
.在四面体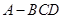 中,若
中,若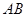 ,
,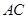 ,
,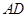 两两垂直,
两两垂直,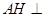 底面
底面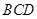 ,垂足为
,垂足为 ,则类似的结论是什么?并说明理由.
,则类似的结论是什么?并说明理由.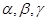 ,三条直线a,b,c共点,知:
,三条直线a,b,c共点,知: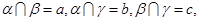 且
且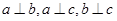 。求证:
。求证:  、
、 是两个不同的平面,
是两个不同的平面,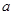 、
、 是两条不同的直线,给出下列4个命题,其中正确命题是( )
是两条不同的直线,给出下列4个命题,其中正确命题是( ) 、
、 、
、 表示三条不同的直线,
表示三条不同的直线,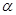 表示平面,给出下列命题:
表示平面,给出下列命题: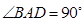 ,AD∥BC, AB="BC=2," AD="4,"
,AD∥BC, AB="BC=2," AD="4," 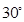 角,E是PD的中点.
角,E是PD的中点. 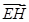 的坐标;
的坐标;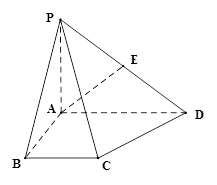
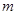 ,
,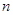 为两条不同的直线,
为两条不同的直线,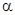 ,
, 为两个不同的平面,则下列命题是真命题的是( )
为两个不同的平面,则下列命题是真命题的是( )