题目内容
本题满分14分)
四棱锥P-ABCD中,底面ABCD为直角梯形,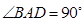 ,AD∥BC, AB="BC=2," AD="4,"
,AD∥BC, AB="BC=2," AD="4,"
PA⊥底面ABCD,PD与底面ABCD成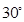 角,E是PD的中点.
角,E是PD的中点.
(1)点H在AC上且EH⊥AC,求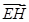 的坐标;
的坐标;
(2)求AE与平面PCD所成角的余弦值;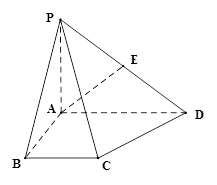
四棱锥P-ABCD中,底面ABCD为直角梯形,
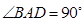 ,AD∥BC, AB="BC=2," AD="4,"
,AD∥BC, AB="BC=2," AD="4," PA⊥底面ABCD,PD与底面ABCD成
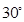 角,E是PD的中点.
角,E是PD的中点. (1)点H在AC上且EH⊥AC,求
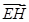 的坐标;
的坐标;(2)求AE与平面PCD所成角的余弦值;

(1)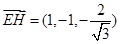 ;(2)
;(2)
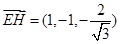 ;(2)
;(2)
第一问以AB,AD,AP分别为x,y,z轴,建立如图所示的坐标系。
则由条件知,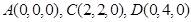
而:PA⊥底面ABCD,PD与底面ABCD成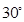 角
角
∴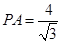 , ∴
, ∴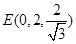 ∴
∴
设 , ∴
, ∴
由EH⊥AC得,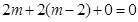 ,解得
,解得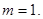
第二问由上得, 而
而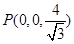 ,
,
∴ ,
, 
记平面PCD的一个法向量为 ,则
,则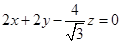 且
且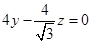
解得 取
取
则
解(1) 以AB,AD,AP分别为x,y,z轴,建立如图所示的坐标系。

则由条件知,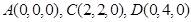 ---------------2分
---------------2分
而:PA⊥底面ABCD,PD与底面ABCD成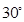 角
角
∴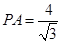 , ∴
, ∴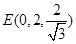 --------------4分
--------------4分
∴
设 , ∴
, ∴
由EH⊥AC得,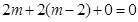 ,解得
,解得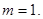 --------------6分
--------------6分
∴所求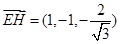 --------------7分
--------------7分
(2)由上得, 而
而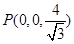 ,
,
∴ ,
,  --------------9分
--------------9分
记平面PCD的一个法向量为 ,则
,则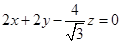 且
且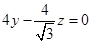
解得 取
取 --------------11分
--------------11分
则 , --------------13分
, --------------13分
设AE与平面PCD所成角为 ,则
,则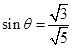 ,则所求的余弦值为
,则所求的余弦值为 --------------14分
--------------14分
则由条件知,
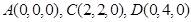
而:PA⊥底面ABCD,PD与底面ABCD成
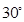 角
角∴
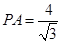 , ∴
, ∴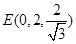 ∴
∴
设
 , ∴
, ∴
由EH⊥AC得,
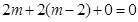 ,解得
,解得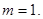
第二问由上得,
 而
而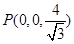 ,
,∴
 ,
, 
记平面PCD的一个法向量为
 ,则
,则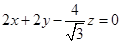 且
且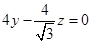
解得
 取
取
则

解(1) 以AB,AD,AP分别为x,y,z轴,建立如图所示的坐标系。

则由条件知,
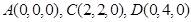 ---------------2分
---------------2分而:PA⊥底面ABCD,PD与底面ABCD成
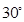 角
角∴
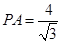 , ∴
, ∴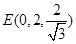 --------------4分
--------------4分∴

设
 , ∴
, ∴
由EH⊥AC得,
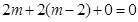 ,解得
,解得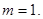 --------------6分
--------------6分∴所求
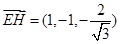 --------------7分
--------------7分(2)由上得,
 而
而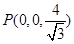 ,
,∴
 ,
,  --------------9分
--------------9分记平面PCD的一个法向量为
 ,则
,则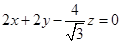 且
且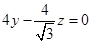
解得
 取
取 --------------11分
--------------11分则
 , --------------13分
, --------------13分设AE与平面PCD所成角为
 ,则
,则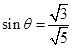 ,则所求的余弦值为
,则所求的余弦值为 --------------14分
--------------14分
练习册系列答案
相关题目
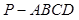 的底面
的底面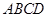 是正方形,侧棱
是正方形,侧棱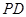 ⊥底面
⊥底面 ,
,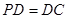 ,
,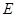 是
是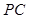 的中点.
的中点. 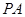 //平面
//平面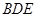 ;
; 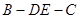 的平面角的余弦值;
的平面角的余弦值;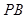 上是否存在点
上是否存在点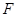 ,使
,使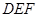 ?若存在,请求出
?若存在,请求出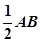 ,N为AB上一点,AB=4AN, M,S分别为PB,BC的中点.
,N为AB上一点,AB=4AN, M,S分别为PB,BC的中点.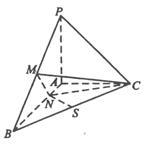
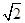 .
.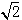 ,PD⊥BC。
,PD⊥BC。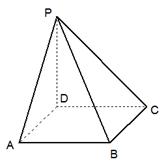
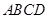 是等腰梯形,
是等腰梯形,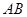 ∥
∥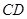 ,
,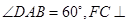 平面
平面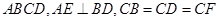 .
.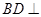 平面
平面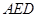 ;
;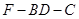 的余弦值.
的余弦值.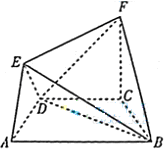
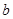 、
、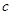 表示两条直线,
表示两条直线,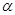 、
、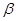 表示两个平面,下列命题中真命题是( )
表示两个平面,下列命题中真命题是( )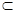
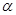 ,
,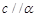 则
则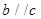 ,
, ,则
,则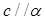
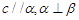 ,则
,则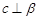
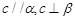 ,则
,则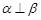
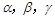 满足
满足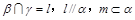 ,
, ,则有
,则有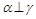 且
且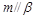
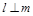
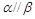 且
且