题目内容
(本小题满分12分)
在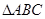 中,若
中,若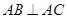 ,
,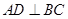 于
于 ,则
,则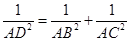 .在四面体
.在四面体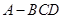 中,若
中,若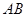 ,
,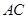 ,
,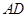 两两垂直,
两两垂直,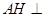 底面
底面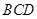 ,垂足为
,垂足为 ,则类似的结论是什么?并说明理由.
,则类似的结论是什么?并说明理由.
在
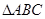 中,若
中,若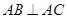 ,
,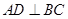 于
于 ,则
,则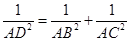 .在四面体
.在四面体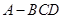 中,若
中,若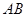 ,
,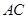 ,
,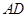 两两垂直,
两两垂直,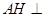 底面
底面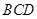 ,垂足为
,垂足为 ,则类似的结论是什么?并说明理由.
,则类似的结论是什么?并说明理由.见解析.
猜想出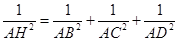 。
。
证明:∵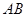 ,
,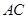 ,
,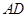 两两垂直,
两两垂直,
∴ 平面
平面 .又∵
.又∵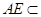 平面
平面 , ∴
, ∴ 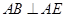 .
.
在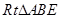 中,有
中,有 ,同理在
,同理在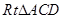 中,
中,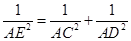 再结合这两个式子问题得证。
再结合这两个式子问题得证。
解:如图,在四面体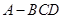 中,若
中,若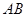 ,
,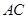 ,
,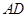 两两垂直,
两两垂直,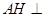 底面
底面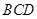 ,垂足为
,垂足为 ,则
,则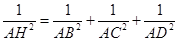 . ………………… 4分
. ………………… 4分
证明如下:
连接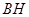 并延长交
并延长交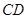 于
于 ,连接
,连接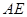 .
.
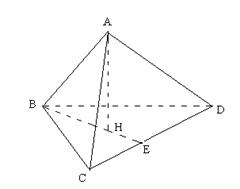
∵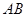 ,
,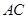 ,
,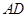 两两垂直,
两两垂直,
∴ 平面
平面 .又∵
.又∵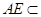 平面
平面 , ∴
, ∴ 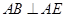 .
.
在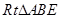 中,有
中,有
 . ①………………… 8分
. ①………………… 8分
又易证 ,
,
∴在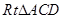 中,
中,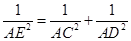 . ② ………………… 10分
. ② ………………… 10分
将②代入①得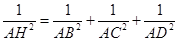 .………………… 12分
.………………… 12分
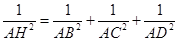 。
。证明:∵
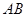 ,
,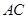 ,
,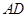 两两垂直,
两两垂直, ∴
 平面
平面 .又∵
.又∵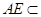 平面
平面 , ∴
, ∴ 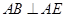 .
.在
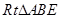 中,有
中,有 ,同理在
,同理在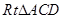 中,
中,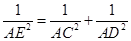 再结合这两个式子问题得证。
再结合这两个式子问题得证。解:如图,在四面体
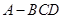 中,若
中,若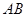 ,
,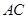 ,
,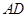 两两垂直,
两两垂直,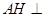 底面
底面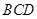 ,垂足为
,垂足为 ,则
,则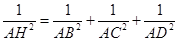 . ………………… 4分
. ………………… 4分证明如下:
连接
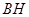 并延长交
并延长交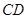 于
于 ,连接
,连接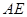 .
.
∵
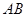 ,
,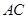 ,
,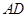 两两垂直,
两两垂直, ∴
 平面
平面 .又∵
.又∵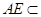 平面
平面 , ∴
, ∴ 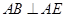 .
.在
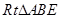 中,有
中,有 . ①………………… 8分
. ①………………… 8分又易证
 ,
,∴在
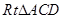 中,
中,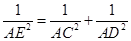 . ② ………………… 10分
. ② ………………… 10分将②代入①得
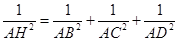 .………………… 12分
.………………… 12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
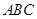 的边长为4,
的边长为4,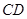 是
是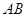 边上的高,
边上的高,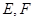 分别是
分别是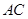 和
和 边的中点,现将△
边的中点,现将△ .
. 的位置关系,并说明理由;
的位置关系,并说明理由; 的余弦值;
的余弦值;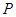 ,使
,使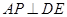 ?如果存在,求出
?如果存在,求出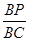 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。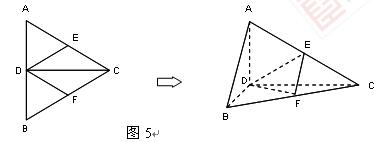
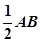 ,N为AB上一点,AB=4AN, M,S分别为PB,BC的中点.
,N为AB上一点,AB=4AN, M,S分别为PB,BC的中点.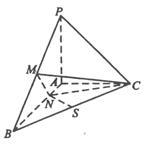
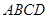 和正
和正
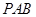 所在平面互相垂直,其中
所在平面互相垂直,其中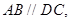
 ,且
,且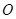 为
为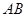 中点.
中点. 
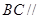 平面
平面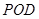 ;
;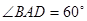 ,求二面角
,求二面角 的余弦值;
的余弦值;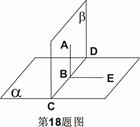
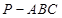 中,直线
中,直线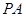 与
与 所成的角的大小为
所成的角的大小为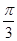
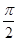
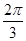
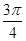
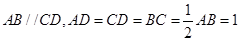 ,E为AB的中点,将
,E为AB的中点,将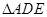 沿
沿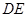 折起,使点A移至点P,若平面
折起,使点A移至点P,若平面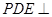 平面
平面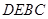 ,则D点到平面
,则D点到平面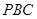 的距离是( )
的距离是( )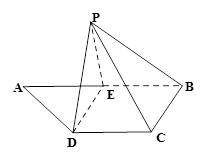
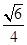

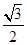

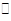 平面
平面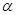 ,点P
,点P
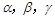 满足
满足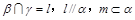 ,
, ,则有
,则有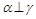 且
且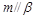
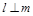
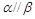 且
且