题目内容
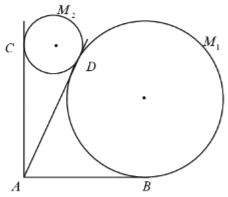
【题目】某景区欲建两条圆形观景步道![]() (宽度忽略不计),如图所示,已知
(宽度忽略不计),如图所示,已知![]() ,
,![]() (单位:米),要求圆M与
(单位:米),要求圆M与![]() 分别相切于点B,D,圆
分别相切于点B,D,圆![]() 与
与![]() 分别相切于点C,D.
分别相切于点C,D.
(1)若![]() ,求圆
,求圆![]() 的半径;(结果精确到0.1米)
的半径;(结果精确到0.1米)
(2)若观景步道![]() 的造价分别为每米0.8千元与每米0.9千元,则当
的造价分别为每米0.8千元与每米0.9千元,则当![]() 多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
【答案】(1)34.6米,16.1米;(2)263.8千元.
【解析】
(1)利用切线的性质即可得出圆的半径;
(2)设∠BAD=2α,则总造价y=0.82π60tanα+0.92π60tan(45°﹣α),化简,令1+tanα=x换元,利用基本不等式得出最值.
(1)连结M1M2,AM1,AM2,
∵圆M1与AB,AD相切于B,D,圆M2与AC,AD分别相切于点C,D,
∴M1,M2⊥AD,∠M1AD=![]() ∠BAD=
∠BAD=![]() ,∠M2AD=
,∠M2AD=![]() ,
,
∴M1B=ABtan∠M1AB=60×![]() =20
=20![]() ≈34.6(米),
≈34.6(米),
∵tan![]() =
=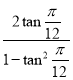 =
=![]() ,∴tan
,∴tan![]() =2﹣
=2﹣![]() ,
,
同理可得:M2D=60×tan![]() =60(2﹣
=60(2﹣![]() )≈16.1(米).
)≈16.1(米).
(2)设∠BAD=2α(0<α<![]() ),由(1)可知圆M1的半径为60tanα,圆M2的半径为
),由(1)可知圆M1的半径为60tanα,圆M2的半径为
60tan(45°﹣α),
设观景步道总造价为y千元,则y=0.82π60tanα+0.92π60tan(45°﹣α)=96πtanα+108π![]() ,
,
设1+tanα=x,则tanα=x﹣1,且1<x<2.
∴y=96π(x﹣1)+108π(![]() )=12π(8x+
)=12π(8x+![]() ﹣17)≥84π≈263.8,
﹣17)≥84π≈263.8,
当且仅当8x=![]() 即x=
即x=![]() 时取等号,
时取等号,
当x=![]() 时,tanα=
时,tanα=![]() ,∴α≈26.6°,2α≈53.2°.
,∴α≈26.6°,2α≈53.2°.
∴当∠BAD为53.2°时,观景步道造价最低,最低造价为263.8千元.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】某地级市共有![]() 中小学生,其中有
中小学生,其中有![]() 学生在
学生在![]() 年享受了“国家精准扶贫”政策,在享受“国家精准扶贫”政策的学生中困难程度分为三个等次:一般困难、很困难、特别困难,且人数之比为
年享受了“国家精准扶贫”政策,在享受“国家精准扶贫”政策的学生中困难程度分为三个等次:一般困难、很困难、特别困难,且人数之比为![]() ,为进一步帮助这些学生,当地市政府设立“专项教育基金”,对这三个等次的困难学生每年每人分别补助
,为进一步帮助这些学生,当地市政府设立“专项教育基金”,对这三个等次的困难学生每年每人分别补助![]() 元、
元、![]() 元、
元、![]() 元,经济学家调查发现,当地人均可支配年收入较上一年每增加
元,经济学家调查发现,当地人均可支配年收入较上一年每增加![]() ,一般困难的学生中有
,一般困难的学生中有![]() 会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生中有
会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生中有![]() 转为一般困难,特别困难的学生中有
转为一般困难,特别困难的学生中有![]() 转为很困难.现统计了该地级市
转为很困难.现统计了该地级市![]() 年到
年到![]() 年共
年共![]() 年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份
年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份![]() 取
取![]() 时代表
时代表![]() 年,
年,![]() 与
与![]() (万元)近似满足关系式
(万元)近似满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数.(
为常数.(![]() 年至
年至![]() 年该市中学生人数大致保持不变)
年该市中学生人数大致保持不变)
|
|
|
|
|
|
|
|
|
|
|
|
其中![]() ,
,![]()
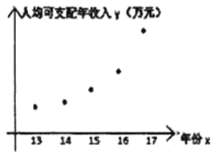
(1)估计该市![]() 年人均可支配年收入;
年人均可支配年收入;
(2)求该市![]() 年的“专项教育基金”的财政预算大约为多少?
年的“专项教育基金”的财政预算大约为多少?
附:对于一组具有线性相关关系的数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]()
|
|
|
|
|
|
|
|
|
|
|
|