题目内容
6.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若$\overrightarrow{AP}$=$\sqrt{2}$$\overrightarrow{PB}$,则椭圆的离心率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 先求出点A,B的坐标,设出点P的坐标,利用$\overrightarrow{AP}$=$\sqrt{2}$$\overrightarrow{PB}$,得到a与c的关系,从而求出离心率.
解答 解:如图,由于BF⊥x轴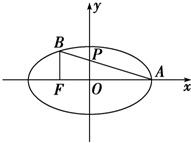 ,
,
故xB=-c,yB =$\frac{{b}^{2}}{a}$,即B(-c,$\frac{{b}^{2}}{a}$),
设P(0,t),又A(a,0),
∵$\overrightarrow{AP}$=$\sqrt{2}$$\overrightarrow{PB}$,
∴(-a,t)=$\sqrt{2}$(-c,$\frac{{b}^{2}}{a}$-t).
∴a=$\sqrt{2}$c,
∴e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
另解:由$\frac{AP}{PB}$=$\frac{AO}{OF}$,即$\sqrt{2}$=$\frac{a}{c}$,
则e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
故选:C.
点评 本题考查椭圆的简单性质以及向量坐标形式的运算法则的应用,属于中档题.

练习册系列答案
相关题目
11. 如图过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”,则椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的“左特征点”M的坐标为( )
如图过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”,则椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的“左特征点”M的坐标为( )
 如图过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”,则椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的“左特征点”M的坐标为( )
如图过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”,则椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的“左特征点”M的坐标为( )| A. | (-2,0) | B. | (-3,0) | C. | (-4,0) | D. | (-5,0) |
18.若Sn,Tn分别是等差数列{an},{bn}的前n项的和,且$\frac{{S}_{n}}{{T}_{n}}$=$\frac{2n+1}{4n-2}$(n∈N*),则$\frac{{a}_{10}}{{b}_{3}+{b}_{18}}$+$\frac{{a}_{11}}{{b}_{6}+{b}_{15}}$=( )
| A. | $\frac{39}{68}$ | B. | $\frac{41}{68}$ | C. | $\frac{39}{78}$ | D. | $\frac{41}{78}$ |
15.已知抛物线的准线方程x=$\frac{1}{2}$,则抛物线的标准方程为( )
| A. | x2=2y | B. | x2=-2y | C. | y2=x | D. | y2=-2x |